1. 制御工学の計算のイメージ

冒頭でも述べたように制御工学（制御理論）では、あるシステムに入力波形を入力したときの出力波形を求めることができます。

実際の計算のイメージを、図1 の手順 ①～④ で説明します。
（図の説明は、「3-1. 制御工学（制御理論）の基礎」で既に行っているので参考にしてください。）

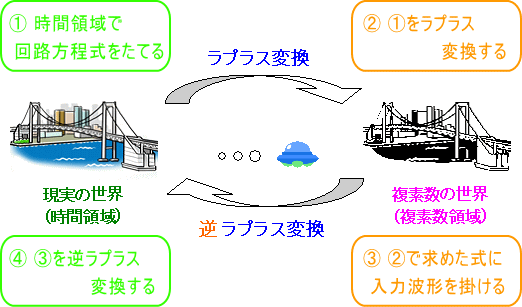
図1. 制御工学の計算のイメージ

まず、時間領域で回路方程式をたてます。これは時間 t の関数となります。（手順①）

そして、その時間 t の関数をラプラス変換することにより、 s領域（s空間）の関数に変換します。時間領域の関数を s領域（s空間）の関数に変換することにより、時間 t の関数のように微分や積分が含まれるなくなります。このことが制御工学の計算の利点で、計算が簡単に行えるようになります。（手順②）

次に、手順②で求めた式に入力波形を掛け合わせます。このとき、入力波形は s領域（s空間）の関数でなければなりません。つまり、時間 t で表された入力波形をラプラス変換したものになります。（手順③）

最後に、手順③で求めた式を逆ラプラス変換することで、時間 t の関数に変換します。（手順④）

以上のようにして、あるシステムに入力波形を入力したときの出力波形を求めることができます。制御工学（制御理論）では、ある入力に対して得られる出力のことを「過渡応答」と呼んでいます。

それでは次に、実際に電気回路を例題に挙げて制御工学の問題を解いてみたいと思います。

2. 制御工学の問題の解き方（過渡応答）

先ほどの「1. 制御工学の計算のイメージ」で説明した手順に沿って、ここでは電気回路の例題を挙げて実際に問題を解いていきましょう。

ちなみに、世の中で使用されている多くの電気回路や電子回路は、制御工学の考え方をもとに設計されているものばかりです。具体的には回路の伝達関数を求めて設計されます。（伝達関数の求め方については、次節「3-4. 伝達関数の求め方」で説明しています。）

さて話を戻して、図2 (a) は抵抗 R とコンデンサ C が直列に接続された回路です。この回路に、時間 t<0 のとき v(t)=0 、t≧0 のとき v(t)=V0 となるステップ状の電圧が入力されたときの電流 i(t) の特性を求めてみましょう。

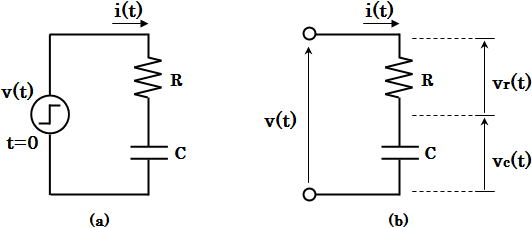
図2. 抵抗とコンデンサの直列回路

まずは先ほど説明した手順①、「時間領域での回路方程式をたてる」です。図2 (b) に示すように、抵抗 R に電流 i(t) が流れたときの電圧 vr(t) は下式(1) で表されます。

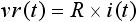
・・・ (1)

また、コンデンサ C に電流 i(t) が流れたときの電圧 vc(t) は下式(2) で表されます。

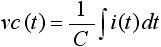
・・・ (2)

抵抗やコンデンサの電圧と電流の関係式については、「3-1. 制御工学（制御理論）の基礎」で既に述べています。

さて、図2 (b) を見ても分かるように v(t) = vr(t) + vc(t) であるため、時間領域での回路方程式は下式(3) のようになります。

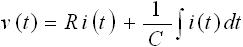
・・・ (3)

次に手順②、「時間 t の関数をラプラス変換する」です。ラプラス変換の特徴の一つとして式(3) のような複数の項を持つ数式、例えば f3(t) = f1(t) + f2(t) のラプラス変換は F3(s) = F1(s) + F2(s) というように表すことができます（ここで、f1(t), f2(t), f(3) のラプラス変換はそれぞれ F1(s), F2(s), F3(s) です）。

また、抵抗やコンデンサの時間領域の式のラプラス変換は、前節「3-2. ラプラス変換」の「2. 抵抗、容量、インダクタのラプラス変換」で述べた通りです。以上より、式(3) のラプラス変換は下式(4) のように表されます。

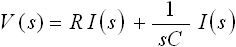
・・・ (4)

今回の例題で求めたいのは電流ですので、式(4) を電流についての式に変形します。式(4) を変形すると下式(5) のようになります。

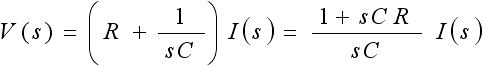
・・・ (5)

よって、電流についての式は下式(6) のようになります。

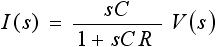
・・・ (6)

次に手順③、「手順②で求めた式に入力波形を掛ける」です。この例題における入力波形は、時間 t<0 のとき v(t)=0 、t≧0 のとき v(t)=V0 となるステップ状の電圧です。前節「3-2. ラプラス変換」で述べたようにステップ関数（ヘビサイド関数）を u(t) とすると、入力波形は V0×u(t) となます。

この入力波形を式(6) に掛け合わせたいのですが、式(6) は s領域（s空間）の関数です。そのため、入力波形 V0×u(t) も s領域の関数にする必要があります。つまり、ラプラス変換する必要があります。V0×u(t) のラプラス変換は V0／s となります。その結果、電流についての式は下式(7) となります。

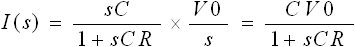
・・・ (7)

さらに式(7) を変形して、下式(8) を得ることができます。

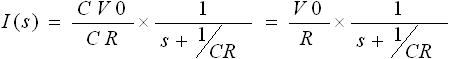
・・・ (8)

さて、いよいよ最後の手順です。手順④は「手順③で求めた式を逆ラプラス変換する」です。当然ですが、式(8) を見ても電流がどのような特性なのか全く分かりません。なぜなら複素数 s の関数だからです。電流の特性を理解するためには、s の関数から時間 t の関数に変換する必要があります。

そのためには逆ラプラス変換をする必要があるのですが、この例題では前節「3-2. ラプラス変換」のラプラス変換表の上から3番目の変換を利用することができます。つまり、 1／(s+a) の逆ラプラス変換は e^(-at) となることを利用します。結果は下式(9) のようになります。

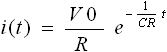
・・・ (9)

以上、式(9) が図2 の回路に振幅 V0 のステップ状の電圧を入力したときの出力の式になります。下図3 に入力波形と出力波形の様子を図示しています。

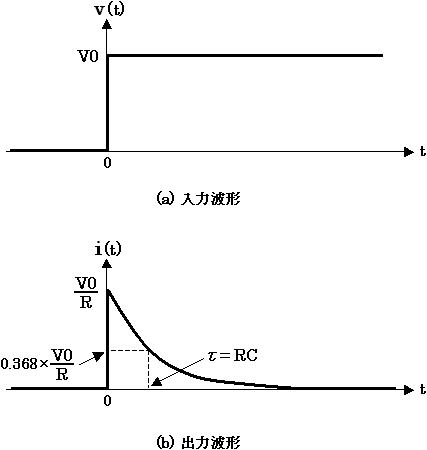
図3. ステップ状の電圧に対する出力

図3 (a) は振幅 V0 のステップ状の入力波形で、同図 (b) は出力波形を表しています。図中の ” τ ” は時定数と呼ばれ、この回路の時定数は τ = RC となります。（時定数とは、出力が最終的な値に落ち着くまでの時間がどの程度早いのかを表す指標です。）

以上、図2 の回路の例題を通して制御工学の問題を解いていきました。制御工学では、任意の入力波形に対する出力波形を求めることができます。次に、制御工学で最も重要な「伝達関数」について少し説明します。

3. 伝達関数

さて、制御工学（制御理論）では「伝達関数」と呼ばれるものを使って、いろいろな特性を調べることができます。伝達関数とは制御工学にとって非常に重要な存在です。

それでは伝達関数とは何か？

s領域（s空間）における入力を X(s) 、出力を Y(s) とすると、伝達関数は Y(s)／X(s) で表されます。先ほどの例題の伝達関数は、式(6) より以下のように求まります。

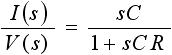
・・・ (10)

制御工学では、「2. 制御工学の問題の解き方（過渡応答）」で説明したように任意の入力波形に対する出力波形を求めることができます。しかし、それは制御工学の ”本題” ではありません。制御工学において更に重要なことは、式(10) のような伝達関数を使って入出力システムの挙動や安定性を評価するところにあります。

それでは次節「3-4. 伝達関数の求め方」で、抵抗やコンデンサ、インダクタといった回路素子で構成された回路の伝達関数の求め方について説明したいと思います。