電子回路設計の基礎 > 3-4. 伝達関数の求め方
伝達関数の求め方
このページでは、抵抗やコンデンサ(容量)、インダクタといった回路素子で構成された回路の伝達関数の求め方について説明します。ちなみに、伝達関数の基礎となる分野は制御工学(制御理論)です。伝達関数は非常に重要で、伝達関数を使って入出力システムの挙動や安定性を評価することができます。
1. 電気回路における伝達関数
前節「3-3. 制御工学の問題の解き方」で説明したように、伝達関数は s領域(s空間)における入力と出力の関係式で、入力を X(s) 、出力を Y(s) とすると Y(s)/X(s) で表すことができます。
前節の例題では、まず時間領域(時間 t の関数)で回路方程式をたて、それからラプラス変換を行って入力 X(s) と出力 Y(s) の関係式を求めました。しかし、これから説明する方法を使えば電気回路から直接、伝達関数を求めることができます。まずは、図1 に伝達関数の求め方の簡単なイメージを示します。
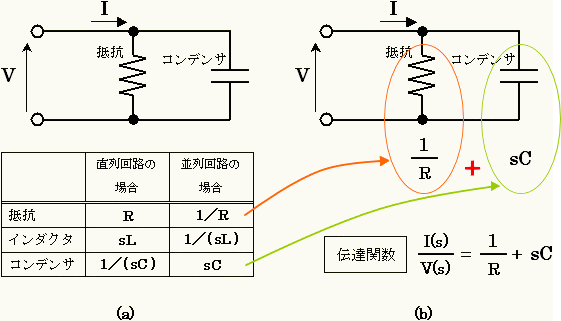
図1. 伝達関数の求め方の簡単なイメージ
例として、図1 (a) の上の段の回路について伝達関数をどのように求めていくか説明します。図の回路は抵抗 R とコンデンサ C で構成されており、入力を電圧 V で出力を電流 I としています。よって、求めるべき伝達関数は s領域(s空間)の関数 I(s)/V(s) になります。
まず、図1 (a) の下の段の表を用意します。この表を使い、それぞれの素子がどのように接続されているかによって、パズルのように数式を組み立てることで伝達関数を求めることができます。あらためて以下に表1 を示します。
表1. 伝達関数を求めるときに必要な数式
| 直列回路の場合 | 並列回路の場合 | |
| 抵抗 | R | 1/R |
| インダクタ | sL | 1/(sL) |
| コンデンサ | 1/(sC) | sC |
それでは実際に伝達関数を求めてみます。図1 の回路図は抵抗とコンデンサの並列回路です。そこで表1 から、抵抗については 1/R を、コンデンサについては sC を選びます。そして、これらの式を足し合わせるだけで伝達関数が求まります。結果は下式(1) の通りです。
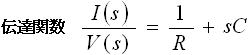
・・・ (1)
以上の例ではパズルのように数式を組み立て、非常に簡単に伝達関数を求めることができました。伝達関数を求めるための流れは理解して頂けたでしょうか?ただし以上で述べたものは簡単な例で、実際に色々な回路の伝達関数を求めるためには、もう少しルールを覚える必要があります。次に、そのルールについて詳しく説明します。
ちなみに、世の中で使用されている多くの電気回路や電子回路は、伝達関数の考え方をもとに設計されているものばかりです。伝達関数の基礎となる分野は制御工学(制御理論)です。制御工学の基礎については、「3-1. 制御工学(制御理論)の基礎」で説明しています。
◆ おすすめの本 - 演習で学ぶ基礎制御工学
↓↓ 内容の一部を見ることができます ↓↓
- 演習を通して、制御工学の内容を理解できる。
- 多くの具体例(電気回路など)を挙げて、伝達関数を導出しているので実践で役に立つ。
- いろいろな伝達関数について周波数応答(周波数特性)と時間関数(過渡特性)を求めており、周波数特性を見て過渡特性の概要を思い浮かべることが出来るように工夫されている。
- ラプラス変換とラプラス逆変換の説明
- 伝達関数の説明と導出方法の説明
- 周波数特性と過渡特性の説明
- システムの安定判別法について
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
2. 電気回路の伝達関数を求めるためのルール
電気回路の伝達関数を求めるためには、本サイトの「2-5. 交流回路(交流理論)の基礎」で説明しているインピーダンスとアドミタンスの計算のルールを利用すれば簡単に覚えることができます。
まずは、表1 の「直列回路の場合」の列の R , sL , 1/(sC) をインピーダンスと呼ぶことにします。そして、「並列回路の場合」の列の 1/R , 1/(sL) , sC をアドミタンスと呼ぶことにします。
ここで念を押しておきたいのですが、インピーダンスやアドミタンスとはもともと電気回路(特に交流回路)の分野で使われる言葉です。ここでは便宜上、こういう名前で呼んでいるのだと認識しておいてください。
表1 をインピーダンスとアドミタンスに置き換えて、再度、表2 に示します。インピーダンスとアドミタンスの関係は常に逆数の関係にありますが、これは非常に重要な特徴です。また、インピーダンスは Z 、アドミタンスは Y という記号で表すことにします。
表2. インピーダンスとアドミタンス
| インピーダンス Z | アドミタンス Y | |
| 抵抗 | R | 1/R |
| インダクタ | sL | 1/(sL) |
| コンデンサ | 1/(sC) | sC |
このように考えると、「3-2. ラプラス変換」の「2. 抵抗、容量、インダクタのラプラス変換」で説明した電流と電圧の関係式から、以下の式(2) , (3) のように表すことができます。
入力を電流 I とし、そのときの出力電圧を V とするとインピーダンス Z を用いて下式(2) のように表すことができます。
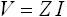
・・・ (2)
一方、入力を電圧 V とし、そのときの出力電流を I とするとアドミタンス Y を用いて下式(3) のように表すことができます。
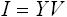
・・・ (3)
さらに新たなルールとして、合成インピーダンスと合成アドミタンスの求め方を覚える必要があります。抵抗、インダクタ、コンデンサ(容量)が直列に接続されているときはそれぞれのインピーダンスを足し合わせ、一方、並列に接続されたときはアドミタンスを足し合わせます。
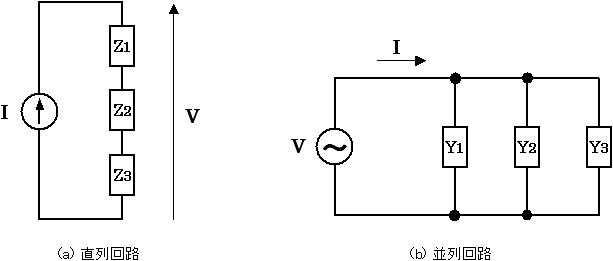
図2. 交流回路
図2 (a) は、抵抗、インダクタ、コンデンサといった素子が直列に接続されている様子を表しており、それぞれのインピーダンスを Z1 , Z2 , Z3 とするならば合成インピーダンス Ztotal は Ztotal = Z1+Z2+Z3 と求まります。この回路に電流 I を流したときの回路の両端にかかる電圧は、式(2) より以下のようになります。
V = (Z1 + Z2 + Z3) × I ・・・ (4)
また、図2 (b) は、回路素子が並列に接続されている様子を表しており、それぞれのアドミタンスを Y1 , Y2 , Y3 とするならば、合成アドミタンス Ytotal は Ytotal = Y1+Y2+Y3 と求まります。この回路に電圧 V をかけたときに回路に流れる全電流は、式(3) より以下のようになります。
I = (Y1 + Y2 + Y3) × V ・・・ (5)
さて、ここで回路をパズルのように解くための「決まり事」について説明します。「決まり事」は以下の通りです。
決まり事(1) ・・・ 求めるものが電圧か電流かで合成インピーダンス Ztotal か合成アドミタンス Ytotal のどちらを求めるか決める。
・ 求める値が電圧の場合 : V = Ztotal × I の合成インピーダンス Ztotal を求める。
・ 求める値が電流の場合 : I = Ytotal × V の合成アドミタンス Ytotal を求める。
決まり事(2) ・・・ 直列接続なら合成インピーダンス、並列接続なら合成アドミタンスを求める。
・ 抵抗が直列接続されている場合 : 合成インピーダンス Ztotal = Z1+Z2+Z3+・・・ を求める。
・ 抵抗が並列接続されている場合 : 合成アドミタンス Ytotal = Y1+Y2+Y3+・・・ を求める。
決まり事(3) ・・・ インピーダンス Z とアドミタンス Y の変換は、お互いを逆数にする。( Z = 1/Y , Y = 1/Z )
それでは、以上の決まり事を使って実際に回路を計算してみましょう。
3. 伝達関数の計算
下図3 の回路は抵抗、インダクタ、コンデンサ(容量)が直列に接続された回路で、電圧 V が与えられています。このとき、抵抗、インダクタ、コンデンサに流れる電流 I を求めてみましょう。
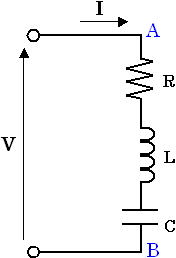
図3. 抵抗、インダクタ、コンデンサで構成された回路
電圧 V が与えられており、求めるものは電流 I であるため「 決まり事(1) 」より I = Ytotal × V の Ytotal を求めます。つまり、A点-B点間の合成アドミタンス Ytotal を求めます。
次に、A点-B点間の回路素子 R , L , C に注目します。それぞれ直列に接続されているため、「 決まり事(2) 」より合成インピーダンス Ztotal を求めます。 Ztotal は下式(6) のようになります。
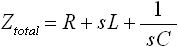
・・・ (6)
さらに式(6) を変形すると、式(7) になります。
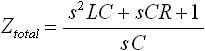
・・・ (7)
さて、始めに「 決まり事(1) 」より、求めるものが電流 I であることから合成アドミタンスを求めると述べました。そこで「 決まり事(3) 」を使って式(7) の合成インピーダンス Ztotal を合成アドミタンスに変換します。合成アドミタンスは下式(8) となります。
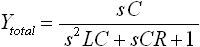
・・・ (8)
伝達関数は、出力/入力で表されます。図3 の例では入力が電圧 V で、出力が電流 I なので式(3) より伝達関数は I/V = Ytotal となります。つまり、式(8) が伝達関数となります。
4. 極と零点(ゼロ点)
伝達関数は一般に、式(9) のような式で表すことができます。
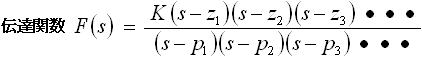
・・・ (9)
式(8) に関しても、分母を因数分解すれば (s - p1) × (s - p2) のような形に変形できます。分子も z=0 で (s - 0) = s と表すことができます。
伝達関数を式(9) のように表したとき、p1 , p2 , p3 ・・・ を” 極 ”、z1 , z2 , z3 ・・・ を” 零点 (ゼロ点)”と呼びます。この極や零点は、「3-6. 周波数特性とボード線図」で説明するように周波数特性を考えるときに役に立ちます。
また、極や零点が複素平面上のどこに存在するかによって、システムの安定性を判断することができます。(本サイトでは、安定性の判別については述べていませんので、教科書や参考書などの本を参考にしてください。)