電子回路設計の基礎 > 2-4. インピーダンスとアドミタンス
インピーダンスとアドミタンス
交流回路の解析は、抵抗、容量、インダクタといった回路素子で構成された回路に正弦波交流(サイン波)の電圧や電流を入力したときの応答についての解析です。交流回路の解析である交流理論では、三角関数(sin, cos, tan)を使うのではなく複素数(実数と虚数を含んだ数)を用います。
交流理論では、インピーダンスとアドミタンスといった概念が登場しますが、このインピーダンスとアドミタンスは複素数で表されます。このページでは、インピーダンスとアドミタンスについて説明します。
1. インピーダンスとアドミタンスとは
「2-2. 容量とインダクタ」で、正弦波交流の電流および電圧入力に対する特徴を述べました。まずはその復習をしてみましょう。
正弦波の電流入力に対する電圧出力の振幅と位相の特徴を表1 にまとめています。 I0 は入力電流の振幅、 V0 は出力電圧の振幅です。
表1. 電流入力に対する電圧出力の振幅と位相
| 素子 | 出力電圧の振幅 | 電流に対する電圧の位相のずれ |
| 抵抗 | 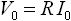 |
位相のずれなし |
| インダクタ | 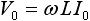 |
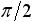 (90度)進み (90度)進み |
| 容量 | 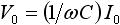 |
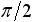 (90度)遅れ (90度)遅れ |
一方、正弦波の電圧入力に対する電流出力の振幅と位相の特徴は表2 のようになります。 V0 は入力電圧の振幅、 I0 は出力電流の振幅です。
表2. 電圧入力に対する電流出力の振幅と位相
| 素子 | 出力電圧の振幅 | 電流に対する電圧の位相のずれ |
| 抵抗 | 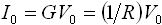 |
位相のずれなし |
| インダクタ | 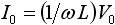 |
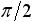 (90度)遅れ (90度)遅れ |
| 容量 | 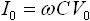 |
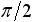 (90度)進み (90度)進み |
さて、これら表1 、表2 の特徴は複素数を使ってうまく表現することができます。まず、表1 の特性についてですが、抵抗、インダクタ、容量をそれぞれ ZR 、 ZL 、 ZC とし、下式(1) のように定義します。
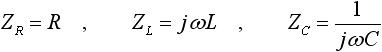
・・・ (1)
ここで、 ZR 、 ZL 、 ZC をまとめて Z と表すと、表1 の特徴を下式(2) で表すことができます。
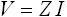
・・・ (2)
I は入力電流、 V は出力電圧です。 I を、振幅が I で位相のずれが 0度の基準と考えると、それぞれ図1 のようになります(複素数の特徴より、 1/j = -j となる)。
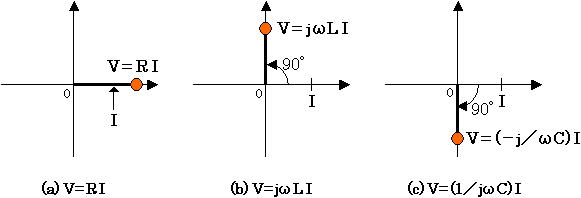
図1. 抵抗、インダクタ、容量の複素数表現
図1 より、式(1) 、式(2) が表1 の特徴を表していることが分かります(複素数の特徴については「2-3. 交流回路と複素数」を参照にしてください)。この Z をインピーダンスと呼んでいます。
一方、表2 の特性についてですが、抵抗、インダクタ、容量をそれぞれ YR 、 YL 、 YC とし、下式(3) のように定義します。
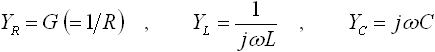
・・・ (3)
ここで、 YR 、 YL 、 YC をまとめて Y と表すと、表2 の特徴を下式(4) で表すことができます。
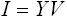
・・・ (4)
この式(3) 、式(4) が表2 の特徴を表します。この Y をアドミタンスと呼んでいます。
2. インピーダンスとアドミタンスの計算
先ほどの、「1. インピーダンスとアドミタンスとは」で述べたことをまとめると、下表3 のようになります。表3 を見ると分かりますが、インピーダンスとアドミタンスの関係は常に逆数の関係にあります。
表3. インピーダンスとアドミタンス
| インピーダンス | アドミタンス | |
| 抵抗 | R | 1/R (= G ) |
| インダクタ | jωL | 1/(jωL) |
| コンデンサ | 1/(jωC) | jωC |
それでは、ここでインピーダンスとアドミタンスを使って簡単な交流回路の計算をしてみましょう。図2 は抵抗と容量で構成された回路で、交流電圧 V が与えられます。このとき、抵抗と容量に流れる電流 I を求めましょう。
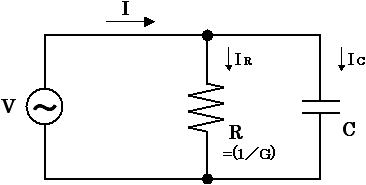
図2. 抵抗と容量で構成された回路
ここで、入力される交流電圧 V は複素数 V+j0 と考えてください。つまり図3 (a) のように時間 t=0 のとき位相が 0度で、基準となっています。図3 では、複素数(インピーダンスとアドミタンス)の様子と同時に、理解しやすいように正弦波の様子も示しています。
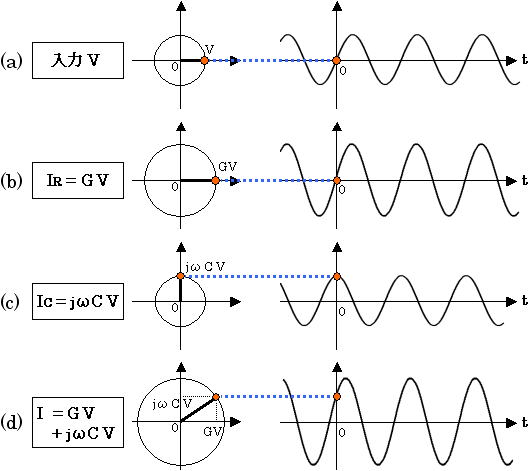
図3.交流回路の計算例
図2 の回路図を見ると分かるように、抵抗 R と容量 C に同じ正弦波交流(サイン波)の電圧がかかっています(図3 (a) )。よって式(3) と式(4) より、抵抗に流れる電流 IR と容量に流れる電流 IC は下式(5) のように求められます(図3 (b) と (c) )。

・・・ (5)
IR は入力に対しての位相のずれはなく、 IC は正弦波の電圧入力に対して電流出力は 90度位相が進みます。(コンダクタンス G について知りたい場合は、「2-1. 電気回路の基礎」を参照にしてください。)
そして合計の電流 I は、図3 (d) のような正弦波となり、振幅 I0 と位相のずれ Φ は下式(6) , (7) で求まります。
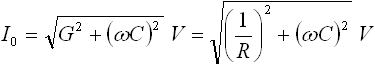
・・・ (6)
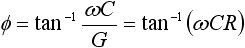
・・・ (7)
以上がインピーダンスとアドミタンスの説明ですが、理解できましたでしょうか?一応、下に初心者向けの良書を紹介しておきます。インピーダンスやアドミタンスの説明もかなり丁寧に分かりやすく解説してあります。
◆ 初心者におすすめの本 - 図解でわかるはじめての電気回路
- 説明の図も多く、分かりやすいです。
- これから電気回路を学ぶ方にお勧め、初心者必見の本です。説明がかなり丁寧です。
- 容量の原理について、クーロンの法則や静電誘導の原理といった説明からしっかりとされています。
- インダクタの原理について、ファラデーの法則やフレミングの法則といった説明からしっかりとされています。
- インピーダンスとアドミタンスについても、各素子に関して丁寧に説明されています。
- 抵抗、容量、インダクタ、トランスの説明
- インピーダンスやアドミタンスの説明、計算方法
- 三相交流の説明
- トランジスタやダイオードといった半導体素子の説明と正弦波交流に対する動作
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
それでは次に、複素数(インピーダンスとアドミタンス)を使う利点について説明するために図2 の回路を三角関数(sin , cos)を使って計算してみることにします。また次節に進みたい方は、飛ばして頂いても構いません。次節「2-5. 交流回路(交流理論)の基礎」では、交流回路をパズルのように解くための「決まり事」について説明していきます。
3. 三角関数を使って計算した場合
本章では折に触れて、複素数(インピーダンスとアドミタンス)を使う理由は交流回路の計算を非常に簡単に行うことができるためと説明してきました。
そこでここでは、先ほどの図2 の回路を三角関数(sin , cos)を使って解いてみることにします。インピーダンスとアドミタンスを使った方が楽に交流回路の計算を行うことがわかるはずです。図2 の回路を図4 に再び示します。
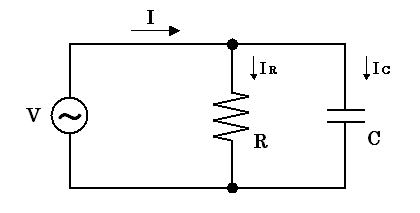
図4. 抵抗と容量で構成された回路
三角関数(sin, cos)を用いた計算を行ってみます。ここで、容量(コンデンサ)の特性について説明します。コンデンサには電荷が蓄えられており、電圧が時間的に変化すると電荷も比例して変化することから、
Q(t) = C × V(t)
と表されます(Q:電荷、C:容量値、V:電圧)。一方、電流とは電荷の時間的な変化であることから、
I(t) = dQ(t)/dt
と表されます。(I:電流)よって、容量の電流と電圧の関係式は以下のようになります。
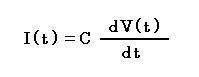
さて、話を本題に戻して、図3 の回路を三角関数を用いて解きます。入力される交流電圧 V を sin(ωt) とすると、抵抗に流れる電流 IR は 1/R × sin(ωt) となります。また、コンデンサに流れる電流 IC は C×(d sin(ωt))/(dt) = ωC × cos(ωt) となります。よって、抵抗と容量に流れる電流 I は、以下のようになります。
I = IR + IC = 1/R × sin(ωt) + ωC × cos(ωt) ・・・ (1)
次に、この式を I = A×sin(ωt + Φ) という形にするために加法定理を用います。加法定理の中に以下の式があります。
sin(a+b) = sin(a)×cos(b) + cos(a)×sin(b)
を用いると下の式が求まります。
I = A×sin(ωt + Φ) = A×sin(ωt)×cos(Φ) + A×cos(ωt)×sin(Φ)
この式と式(1) を比較すると下式が得られます。
A×cos(Φ) = 1/R , A×sin(Φ) = ωC ・・・ (2)
この式から Φ を消去し A を求めるため、上の2式を2乗して足します。
(sinΦ)^2 + (cosΦ)^2 = 1 より、A は以下のように求まります。
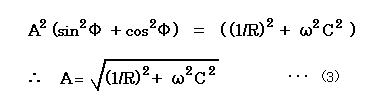
今度は A を消去し Φ を求めるために、式(2) の A×sin(Φ) を A×cos(Φ) で割ります。
(sinΦ)/(cosΦ) = tanΦ より、Φは以下のように求まります。
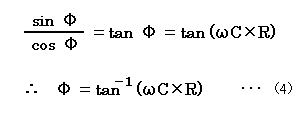
よって、図3 の回路に sin(ωt) の正弦波の電圧を入力したときに流れる電流は下式で表されます。
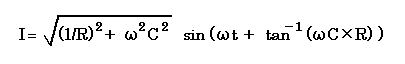
つまり、振幅 1 で位相のずれ 0 の入力に対して、出力は振幅 A ( ・・・ 式(3) ) で位相のずれ Φ ( ・・・ 式(4) ) となります。このように、交流理論ではわざわざ三角関数を用いて計算する必要がありません。もっと簡単にインピーダンス、アドミタンスという複素数の四則演算(+, -, ×, ÷)で、回路に正弦波交流(サイン波)を入力したときの応答を求めることができるのです。
以上が、インピーダンスとアドミタンスの説明です。複素数を使うことにより交流回路の計算が簡単になることが理解できたと思います。それでは、次節「2-5. 交流回路(交流理論)の基礎」では、交流回路をパズルのように解くための「決まり事」について説明していきます。