電子回路設計の基礎(実践編)> 3-1. 矩形波(方形波)を作る
矩形波(方形波)を作る
矩形波(方形波とも言う)は電子工学や信号処理の分野でよく使われる波形の一つです。本章では電子工作を通して矩形波(方形波)発生回路を作ります。この回路を学ぶことで、抵抗分圧やRC回路といった電子回路の基本的な要素回路を理解することができます。
1. 矩形波発生回路の作成に必要な部品
本章で作成する矩形波発生回路(方形波発生回路)を作成するために必要な部品を、以下にリストアップします。実践編 第3章「矩形波 発生回路」で学習するために必要な部品です。
| 部品名 | 値 | 数量 |
| 抵抗 | 2.2 kΩ | 3 |
| 抵抗 | 10 kΩ | 1 |
| 抵抗 | 33 kΩ | 2 |
| コンデンサ | 0.1 μF | 2 |
| オペアンプ | 1 | |
| 可変抵抗器 | 100 kΩVR | 1 |
※ 部品の入手方法は実践編 第1章「1-4. 電子部品などの揃え方」をご参照ください。
※ 電圧測定や波形観測のための測定器については同じく第1章「1-3. 必要な工具・測定器」をご参照ください。
ご存知の方もいると思いますが、まず始めに矩形波(方形波)とはどのようなものかについて説明をします。図1に示すのが矩形波と呼ばれるものです。
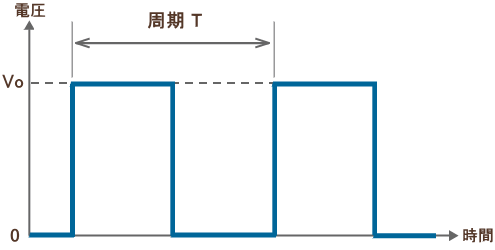
図1. 矩形波(方形波)
矩形波とは、上図のように 0V とある電圧 Vo を周期的に繰り返す波形のことを言います。図中の Vo を「振幅」といい、T を「周期」といいます。また、周期の逆数、つまり 1/T を「周波数」といいます。
それでは次に、矩形波発生回路(方形波発生回路)の概要について説明します。
◆ 本の紹介 (検索もできます。)
○ amazonでネット注文できます。
2. 矩形波(方形波)発生回路の概要
図2に示すのが矩形波発生回路(方形波発生回路)の回路図です。この回路には抵抗やコンデンサに加えて、オペアンプが使用されています(三角形のシンボル)。電子回路においてオペアンプは、言わば「万能回路」といったもので、有りと有らゆる電子回路に使用される部品です。
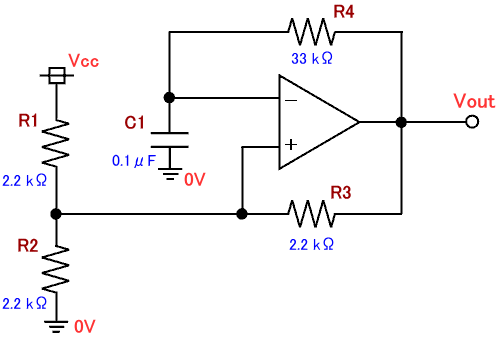
図2. 矩形波(方形波)発生回路の回路図
当サイトの実践編では、オペアンプを理解すると同時に、電気回路や制御工学といった基礎知識を身に付けることができるような構成にしています。
さて、本章で用いられるオペアンプは「コンパレータ(比較器)」として動作します。基礎編「5-2. オペアンプの特徴」でも説明していますが、オペアンプの特性は図3 のような特性です。
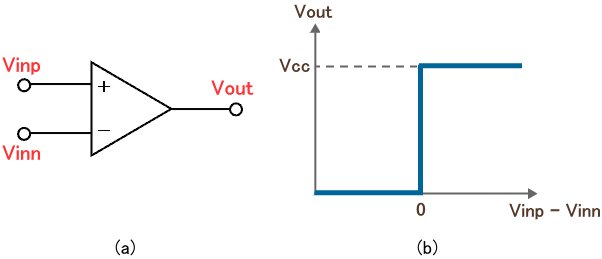
図3. オペアンプの特性
図3 (a) はオペアンプのシンボル図、同図 (b) はオペアンプの特性を表したものです。
オペアンプの2つの入力端子 Vinp と Vinn に関して Vinp - Vinn が正の値(0より大きい値)なら、出力端子 Vout は電源 Vcc に張り付きます。一方、Vinp - Vinn が負の値(0より小さい値)なら、出力端子 Vout は 0V に張り付きます。
本章で学習する矩形波発生回路(方形波発生回路)は、オペアンプがコンパレータ(比較器)として働き、出力電圧 Vout が正電源と負電源を周期的に繰り返すことにより矩形波(方形波)となります。
当サイトの実践編は正電源 = 約 6V 、負電源 = 0V であるため、約 6V と 0V を周期的に繰り返す矩形波(方形波)となります。
なお、オペアンプは通常、フィードバック(負帰還)と呼ばれる手法を用いて回路が構成されるのですが、コンパレータとして使用する場合はフィードバックを用いません。コンパレータは、オペアンプの特殊な使い方と言えます。
フィードバックを用いたオペアンプに関しては、第4章以降で説明します。
3. 本章「矩形波 発生回路」の流れ
このページでは、本章で学習する「矩形波 発生回路」の概要について述べてきました。次のページ以降から具体的に順を追って学習を進めていきます。以下に 3-2. 以降の学習の流れを示します。
- 3-2. 抵抗分圧回路
- 3-3. コンパレータ(比較器)
- 3-4. 矩形波(方形波)発生回路
- 3-5. RC回路と時定数
- 3-6. 矩形波(方形波)発生回路の理論的な理解
「3-2. 抵抗分圧回路」では、抵抗を組み合わせることで任意の電圧を作り出す「抵抗分圧」の動作について、実際に回路を構成しながら学びます。
「3-3. コンパレータ(比較器)」では、2つの入力された電圧を比較することができる回路について学びます。このコンパレータの動作が理解できれば、矩形(方形波)波発生回路の理解に大きく近づきます。
「3-4. 矩形波(方形波)発生回路」では、抵抗分圧とコンパレータの原理を利用した矩形波(方形波)発生回路を実際に構成します。回路の出力端子から矩形波(方形波)を確認することが出来れば、正しく回路を構成できたことになります。
「3-5. RC回路と時定数」では、矩形波(方形波)の周波数を決めている「時定数」について説明します。時定数は大きくなれば周波数は低く、時定数が小さくなれば周波数は高くなります。時定数の理論的な導出方法を学ぶと共に、実際に回路を構成しながらRC回路と時定数の関係を理解します。
「3-6. 矩形波(方形波)発生回路の理論的な理解」では、矩形波(方形波)発生回路の周波数の数式を理論的に求めていきます。周波数を求める数式を導出できれば、必要な周波数に回路を設計することが容易になります。回路の動作を理論的に理解できてこそ、電子回路を設計できると言えると思います。
それでは、以上で述べた内容に従って矩形波発生回路を学習していきましょう。