1. 積分回路とは

図1 (a) に示すのが、積分回路（積分器）です。図に示すように、積分回路はオペアンプと抵抗、コンデンサで構成されます。実際に使用するときには、R2 の抵抗値は R1 に比べて大きな値の抵抗を用います。また、Vb はバイアス電圧を与えるための端子です。

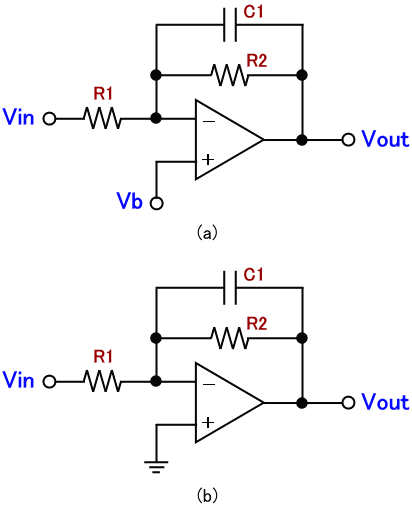
図1. 積分回路（積分器）

バイアス電圧 Vb は直流電圧で、正しく回路が動くために適切に一定の電圧値が設定されます。そのため、バイアス電圧は省略され同図 (b) のようにしばしば回路図が描かれます。バイアス電圧を入力すべき端子はグランドに接続されていますが、これは交流電圧の成分は何も入力されていないという意味で、適切にバイアス電圧が入力されていることを前提としています。

図1 の回路の伝達関数は式(1) のように表されます。

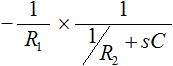
・・・ (1)

先ほども述べたように、R2 は大きな値の抵抗を用います。式(1) の値をみても分かる通り、R2 の値が大きいほど 1/R2 の値は小さくなります。この 1/R2 の値が s×C の値に対して十分に小さければ、式(1) は下式のように表すことができます。

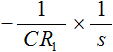
・・・ (2)

基礎編「3-2. ラプラス変換」で説明していますが、1/s は積分であることを表しています。1/s を逆ラプラス変換して時間領域の式にすると、積分の式になるのです。

それゆえ、図1 の回路は「積分回路（または積分器）」と呼ばれます。

2. 積分回路の理論的な理解

積分回路（積分器）は式(1) のように表すことができると説明しましたが、ここからは少し理論的な話をしたいと思います。

このページは実験のページではありませんので、興味がある方は参考にしてください。理論的な理解がなくても、特に支障はありませんので次のページ「5-3. 三角波発生回路を作る」に進んで頂いても構いません。

それでは始めます。

式(1)の説明のときに、「1/R2 の値が s×C の値に対して十分に小さければ」式(2) が求まると述べました。まずはこの点について補足します。

s というのは「3-6. 周波数特性とボード線図」で説明したように、周波数特性を見るときには s=jω と表せます。ここで j は大きさ 1 の虚数です。よって周波数特性で考えるとき、式(2) のようになる条件は「1/R2 の値が ω×C の値に対して十分に小さい」ということになります。

以上のことを踏まえて、式(1) および式(2) の周波数特性を考えてみましょう。図2 (a) が式 (1)、同図 (b) が式 (2) の周波数特性です。

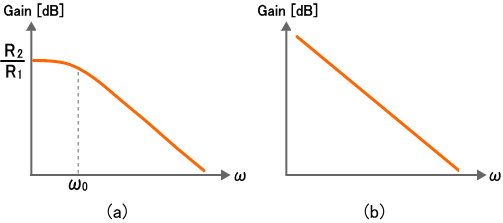
図2. 積分の周波数特性

式(1) の周波数特性は図2 (a) のようにカットオフ周波数 ω0 = 1/(C×R2) のローパス特性です。一方、同図 (b) は理想の積分特性です。つまり、図1 の積分回路は、カットオフ周波数より十分高い周波数で使用しなければ積分回路として動作しないということです。

積分回路に入力される周波数 ω がカットオフ周波数より十分高いことを数式で表すと、ω >> 1/(C×R2) となり、変形すると 1/R2 << ω×C となります。これは式(1) を式(2) のように表すための条件と一致することに気付くと思います。

次に、式(2) が図3 のようなステップ状の関数に対して、どのような動作をするのかについて理論的に説明したいと思います。

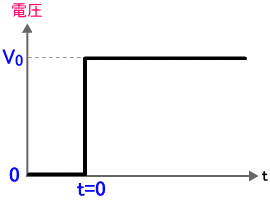
図3. ステップ関数

「3-2. ラプラス変換」で説明しましたが、図3 のようなステップ関数を s で表すと V0/s となります。積分回路に図3 のようなステップ上の波形を入力した場合、出力波形は式 (2) と V0/s を掛けた結果となります。

つまり、-V0/(C×R1) × 1/(s^2) となります。ここで s の2乗の逆ラプラス変換は時間 t ですので、積分回路の出力の式は -V0/(C×R1) × t となります。この式からも分かるように、時間 t に対して線形に変化します。

以上の結果から、積分回路にステップ状の波形を入力した場合、時間変化に対して出力の電圧が線形に変化することが分かります。これが、きれいな三角波を作ることができる理由です。