電子回路設計の基礎 > 2-2. 容量とインダクタ
容量とインダクタ
このページでは、交流回路で用いられる容量(コンデンサ)とインダクタ(コイル)の特徴について説明します。容量やインダクタは、正弦波交流(サイン波)の入力に対して位相が 90度進んだり遅れたりするのが特徴です。ちなみに電気回路では抵抗も使われますが、抵抗は正弦波交流の入力に対して位相の変化はありません。
1. 容量(コンデンサ)の特徴
まず始めに、容量の特徴について説明します。「容量」というより「コンデンサ」といった方が分かるという人もいるでしょう。以下、「容量」で統一します。
図1 (a) は容量のイメージで、容量の両端に電圧 V(t) がかかっている様子を表しています。このとき容量に電荷が蓄えられます。
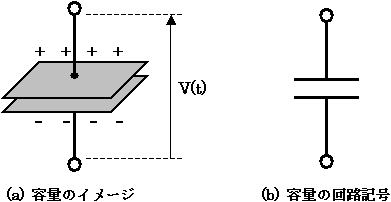
図1. 容量のイメージと回路記号
容量は、電圧が時間的に変化するとそれに比例して電荷も変化するという特徴を持ちます。よって、下式(1) が容量の特徴を表す式ということになります。
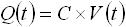
・・・ (1)
Q は電荷量、 C は容量値、 V は電圧です。Q(t) や V(t) の (t) は時間 t の関数であることを表し、電荷量と電圧は時間的に変化します。
一方、電流とは電荷の時間的な変化であることから下式(2) のように表されます( I は電流)。
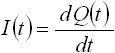
・・・ (2)
よって、式(2) に式(1) を代入すると、容量の電流と電圧の関係式は以下のようになります(式(3) )。
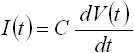
・・・ (3)
式(3) は、容量に電圧をかけたときの電流値について表したものですが、両辺を積分することにより、電流を与えたときの電圧値を表す式に変形できます。下式(4) がその式になります。
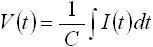
・・・ (4)
以上が容量の特徴です。
2. インダクタ(コイル)の特徴
次に、インダクタの特徴について説明します。インダクタは「コイル」ととも言われますが、ここでは「インダクタ」で統一します。図1 (a) はインダクタのイメージで、インダクタに流れる電流 I(t) の変化に伴い逆起電力が発生する様子を表しています。
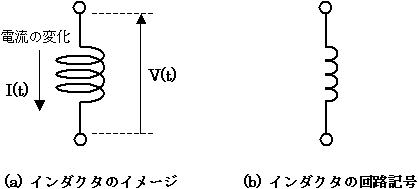
図2. インダクタのイメージと回路記号
インダクタは、電流の時間的な変化量(電流を時間で微分した値)に比例して、逆起電力が発生するという特徴を持ちます。よって、下式(5) がインダクタの特徴を表す式ということになります。
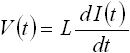
・・・ (5)
ここで L はインダクタンスと呼ばれる定数です。式(5) は、インダクタに電流を流したときの電圧値について表したものですが、両辺を積分することにより、電圧を与えたときの電流値を表す式に変形できます。下式(6) がその式になります。
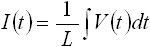
・・・ (6)
以上がインダクタの特徴です。その他、容量やインダクタ以外に電気回路では変成器(トランス)という素子も登場しますが、ここでは紹介致しませんのでご了承ください。
当サイトでは、容量やインダクタの構成や原理についてあまり詳しく述べていませんが、必要があれば以下の本を参考にしてください。初心者向けで最も人気があり、分かりやすい本です。
◆ 初心者におすすめの本 - 図解でわかるはじめての電気回路
- 説明の図も多く、分かりやすいです。
- これから電気回路を学ぶ方にお勧め、初心者必見の本です。説明がかなり丁寧です。
- 容量の原理について、クーロンの法則や静電誘導の原理といった説明からしっかりとされています。
- インダクタの原理について、ファラデーの法則やフレミングの法則といった説明からしっかりとされています。
- インピーダンスとアドミタンスについても、各素子に関して丁寧に説明されています。
- 抵抗、容量、インダクタ、トランスの説明
- インピーダンスやアドミタンスの説明、計算方法
- 三相交流の説明
- トランジスタやダイオードといった半導体素子の説明と正弦波交流に対する動作
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
3. 正弦波交流の入力に対する位相の変化
交流回路では角速度 ω 、振幅 A の正弦波交流(サイン波)の入力 A×sin(ωt) に対して、出力は振幅と位相のみが変化すると「2-1. 電気回路の基礎」で述べました。
ここでは、電圧および電流の正弦波入力に対して抵抗、容量、インダクタといった素子の出力がどのようになるのかについて説明します。この特徴を調べることは、「2-4. インピーダンスとアドミタンス」を理解する上で非常に重要となります。
まずは、正弦波入力に対する結果を表1 および表2 にまとめています。その後に、結果の導出についても記載しているので参考にしてください。
正弦波の電流入力に対する電圧出力の振幅と位相の特徴を表1 にまとめています。 I0 は入力電流の振幅、 V0 は出力電圧の振幅です。
表1. 電流入力に対する電圧出力の振幅と位相
| 素子 | 出力電圧の振幅 | 電流に対する電圧の位相のずれ |
| 抵抗 | 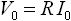 |
位相のずれなし |
| インダクタ | 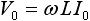 |
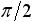 (90度)進み (90度)進み |
| 容量 | 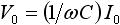 |
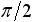 (90度)遅れ (90度)遅れ |
一方、正弦波の電圧入力に対する電流出力の振幅と位相の特徴は表2 のようになります。 V0 は入力電圧の振幅、 I0 は出力電流の振幅です。
表2. 電圧入力に対する電流出力の振幅と位相
| 素子 | 出力電圧の振幅 | 電流に対する電圧の位相のずれ |
| 抵抗 | 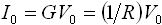 |
位相のずれなし |
| インダクタ | 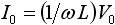 |
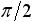 (90度)遅れ (90度)遅れ |
| 容量 | 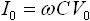 |
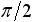 (90度)進み (90度)進み |
G はコンダクタンスと呼ばれるもので、「2-1. 電気回路の基礎」(2-1. の 4. 回路理論における直流回路の計算)で説明しています。位相の「進み」や「遅れ」のイメージを図3 に示しています。
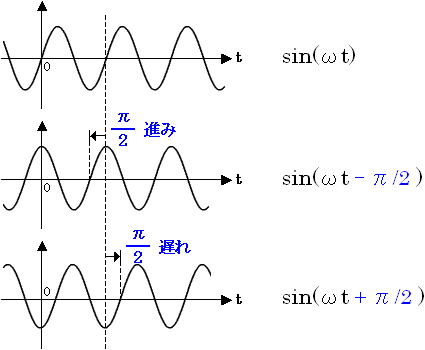
図3. 正弦波の進みと遅れのイメージ
以下、表1 と表2 の内容の導出について、以下に示します。
電圧入力 V(t) を式(7) 、電流入力 I(t) を式(8) として容量とインダクタの出力がどのようになるかを見ていきたいと思います。
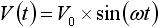
・・・ (7)
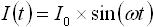
・・・ (8)
まずは容量についてです。式(3) は容量の両端に入力電圧 V(t) がかかっているときの出力 I(t) の式です。容量の両端に正弦波の入力電圧がかかっているときの出力を求めるために、式(3) に式(7) を代入します。すると下式(9) を得ることができます( sin(ωt) の微分は ω×cos(ωt) となる)。
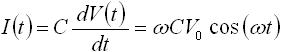
・・・ (9)
cos(ωt) は、 sin(ωt) に対して位相が 90度( π/2 )遅れた状態なので、式(9) は下式(10) のように置き換えることができます。
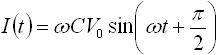
・・・ (10)
一方、式(4) は容量に入力電流 I(t) を流したときの出力 V(t) の式です。入力電流 I(t) を正弦波としたときの出力を求めるために、式(4) に式(8) を代入します。すると下式(11) を得ることができます( sin(ωt) の積分は -1/ω×cos(ωt) となる)。
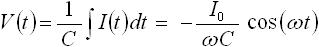
・・・ (11)
-cos(ωt) は、 sin(ωt) に対して位相が 90度( π/2 )進んだ状態なので、式(11) は下式(12) のように置き換えることができます。
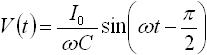
・・・ (12)
次にインダクタについてです。式(5) はインダクタに時間的に変化する電流 I(t) が流れているときの出力 V(t) の式です。入力電流 I(t) を正弦波としたときの出力を求めるために、式(5) に式(8) を代入します。すると下式(13) を得ることができます( sin(ωt) の微分は ω×cos(ωt) となる)。
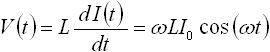
・・・ (13)
cos(ωt) は、 sin(ωt) に対して位相が 90度( π/2 )遅れた状態なので、式(13) は下式(14) のように置き換えることができます。
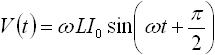
・・・ (14)
一方、式(6) はインダクタに時間的に変化する電流 I(t) がかかっているときの出力 I(t) の式です。入力電圧 V(t) を正弦波としたときの出力を求めるために、式(6) に式(7) を代入します。すると下式(15) を得ることができます( sin(ωt) の積分は -1/ω×cos(ωt) となる)。
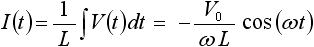
・・・ (15)
-cos(ωt) は、 sin(ωt) に対して位相が 90度( π/2 )進んだ状態なので、式(15) は下式(16) のように置き換えることができます。
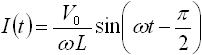
・・・ (16)
以上が容量とインダクタの特徴についてです。次に、「2-3. 交流回路と複素数」の説明を行います。