電子回路設計の基礎 > 4-6. 周波数特性の考え方
周波数特性の考え方
本節「周波数特性の考え方」では、アナログ電子回路において周波数特性とはどういうものなのか、どのように考えればよいかについて述べていきたいと思います。また、周波数特性と過渡特性の関係についても説明します。
1. 周波数特性とは
電子回路の入力には、時間的に変化する電圧や電流の信号が入力されます。例えば図1 のように A という回路があり、その回路に信号を入力したとしましょう。
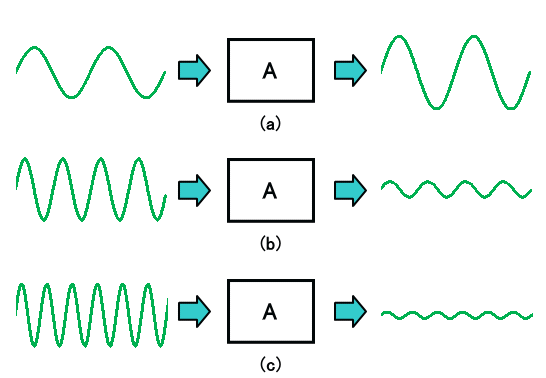
図1. 周波数の異なる信号が入力される様子
入力される信号は、図1 (a), (b), (c) のように、振幅は同じですが周波数の違う信号とします。もちろん (a), (b), (c) とも、電子回路 A は同じものです。
このときの各周波数の入力に対する出力は、それぞれ異なった振幅となります。つまり、入力される信号の周波数によって、出力される信号の振幅が変わるということです。これが周波数特性と呼ばれる特性です。
正確には、周波数特性は振幅についてだけではなく、位相についての変化も含みます。周波数特性は図2 に示すように、横軸を周波数、縦軸を振幅や位相としたグラフでよく表されます。
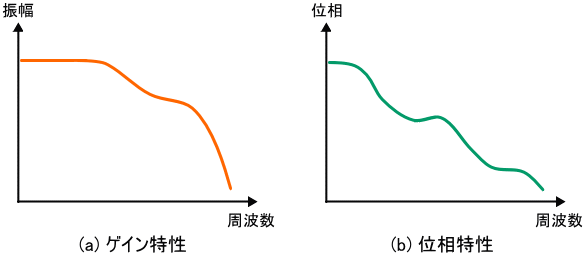
図2. 周波数特性のグラフ
この図2 のグラフは「ボード線図」と呼ばれ、同図 (a) のように振幅と周波数の関係を表したものを「ゲイン特性」といい、同図 (b) のように位相と周波数の関係を表したものを「位相特性」といいます。
周波数特性やボード線図について詳しく知りたい方は、第3章「制御工学 入門」の「3-6. 周波数特性とボード線図」をご参照ください。
さてここでは、周波数特性のゲイン特性について考えてみましょう。ゲイン特性を見ると、どのあたりの周波数が出力にどの程度現われるかが分かります。図2 の例についていえば、周波数が低い領域では信号が衰えずに出力され、周波数が高くなるほど出力される信号が減衰していくことが分かります。
どのような電子回路であれ、周波数特性を必ず持ちます。本章「第4章 アナログ電子回路」のこれまでの説明では、この周波数特性について述べてきませんでした。これは暗黙のうちに、適切な回路動作を行うことができる周波数の信号を扱っているのだと考えてください。実際の回路設計では、回路の周波数特性から扱う信号の周波数範囲が決まります。
また、この周波数特性を意図的に設計し、特定の周波数のみを出力することのできる回路を「フィルタ」と言います。図3 に、代表的なフィルタ特性を示します。
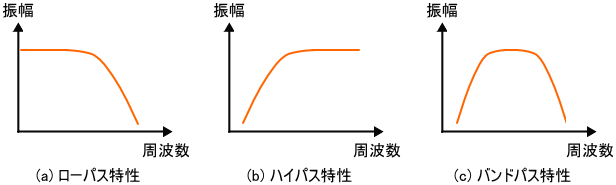
図3. フィルタ特性
図3 (a) のような特性をローパス特性といい、意図的にローパス特性となるように設計した回路をローパス回路といいます。同様に同図 (b), (c) はそれぞれハイパス特性、バンドパス特性といい、このような特性となるように意図的に設計した回路をそれぞれハイパス回路、バンドパス回路といいます。
以上が「周波数特性とは」の説明となりますが、ここで覚えといて頂きたいことは、意図的に設計したかどうかにかかわらず電子回路は必ず何かしらの周波数特性を持つということです。一般的に周波数が低い信号を扱うときは、周波数特性を気にする必要がないケースが多いです。しかし、周波数が高かったり、フィルタなどを使って特定の周波数の信号について処理したりする場合は周波数特性を考えた回路設計が必要となります。
また、次節「4-7. フィードバック(負帰還)」で説明するフィードバックと呼ばれる回路技術を用いる場合も、周波数特性の考え方が必要となります。
さて、これまでの説明では入力される信号がサイン波のみでした。実際の回路動作で入力信号がサイン波だけとは限りません。しかしどのような波形であれ、すべてサイン波の足し合わせで表すことができます。そのことについて、次節「すべての波形はサイン波の足し合わせ」で説明していきたいと思います。
◆ おすすめの本 - 回路シミュレータでストンとわかる! 最新アナログ電子回路のキホンのキホン
↓↓ 内容の一部を見ることができます ↓↓
- 無料配布している回路シミュレータ(LTSpice)を使って、色々な回路の実例を挙げ説明している。
- 本に出てくるシミュレーション用の回路は、Webからダウンロードできる。
- 図が多く用いられており理解しやすい。ほぼ全てのページで、本を開いて左のページに説明、右のページに図という構成で、内容も分かりやすい。
- オームの法則やキルヒホッフの法則、インピーダンスの考え方など、アナログ回路の理解に必要な基礎知識について説明している。
- 電子部品(抵抗、コンデンサ、コイル、トランジスタ、オペアンプなど)の説明と、これら部品の選び方について書いてある。
- 回路シミュレーションを交えて色々な回路の動作について説明している(増幅回路、演算回路、発振回路、フィルタ、電源回路などの基本的なアナログ回路)。
- 変調回路、受信機など少し高度な回路についても、シミュレーションを用いて分かりやすく説明している。
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
2. すべての波形はサイン波の足し合わせ
先ほどの「周波数特性とは」でも述べましたが、電子回路の入力には時間的に変化する電圧や電流の信号が入力されます。その時間的に変化する波形ですが、どのような波形であってもすべてはサイン波の足し合わせであることをご存じでしょうか?
図4 は矩形波のグラフですが、この波形を例に挙げて説明したいと思います。どのような波形でもそうなのですが、この波形も様々な周波数と振幅のサイン波の足し合わせで表されます。
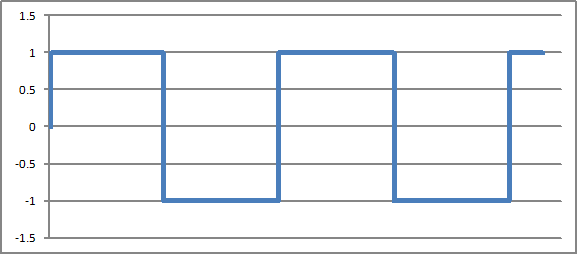
図4. 矩形波のグラフ
下式(1) がその式になります。
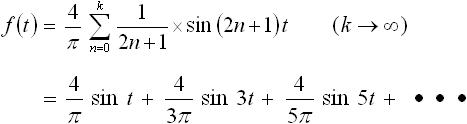
・・・ (1)
この式を見て分かるように、sin t で表される周波数成分と、その整数倍の周波数成分を持つ様々なサイン波の足し合わせです。
この式(1) について、それぞれ k=2, k=8, k=40 として解いた結果を図5 に示します。
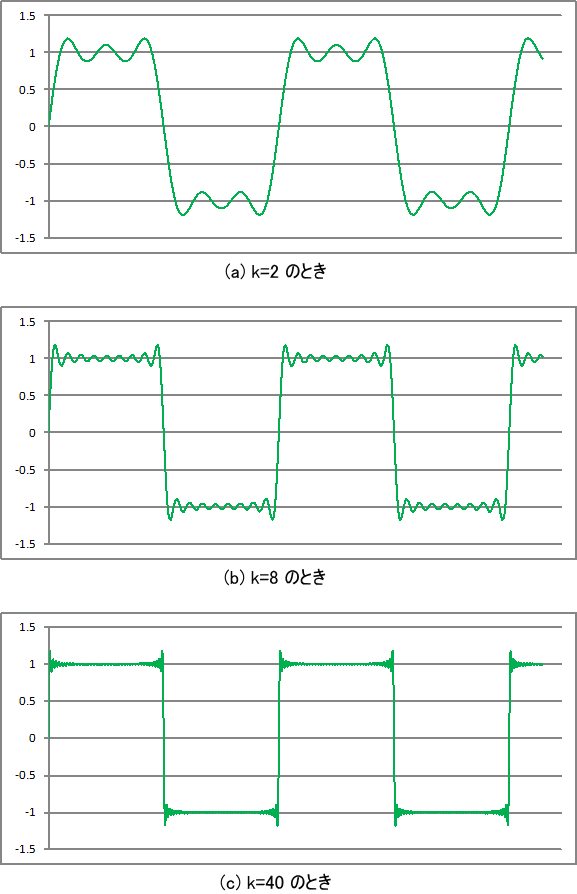
図5. サイン波の足し合わせ(矩形波)
図5 の結果を見ると分かるように、k の値が小さい時はあまり矩形波に近いとは言えませんが、k の値を大きくしていくと矩形波に近づいていきます。
この式(1) を求めるには、フーリエ級数展開という方法を用いる必要があります。式(1) は矩形波の周波数と同じ周波数のサイン波と、その整数倍の周波数のサイン波の足し合わせで成り立っています。
当サイトでは、フーリエ級数展開について詳しくは述べませんが、知りたい方は Web で「フーリエ級数」、「フーリエ級数展開」などと検索すればすぐに調べることができますよ!
ここでは少なくとも、基本波とその整数倍の周波数のサイン波の足し合わせで、あらゆる波形を表すことができるということを覚えて頂ければ十分です。
さて、それではもう一つ例を挙げておきましょう。今度は図6 に示す「のこぎり波」です。
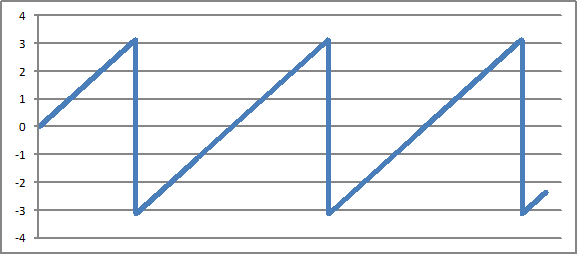
図6. のこぎり波のグラフ
下式(2) がその式になります。
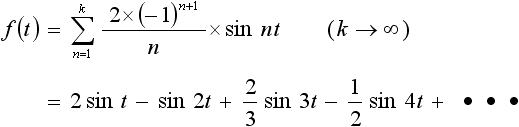
・・・ (2)
この式も sin t で表される周波数成分と、その整数倍の周波数成分を持つサイン波の足し合わせです。この式について、それぞれ k=2, k=8, k=40 として解いた結果を図7 に示します。
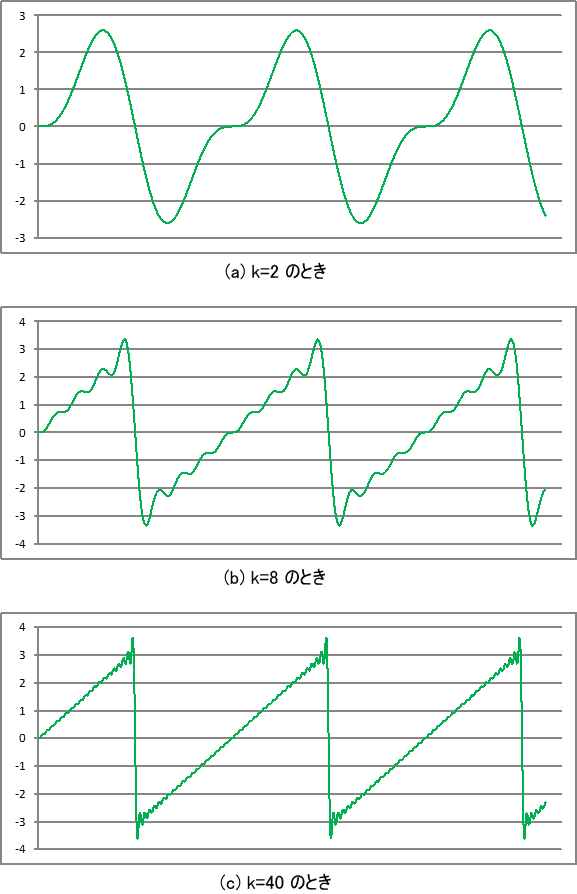
図7. サイン波の足し合わせ(のこぎり波)
以上、すべての波形は様々な周波数と振幅のサイン波の足し合わせで成り立っていることを理解して頂けたと思います。
3. 周波数特性と過渡特性の関係
これまでの説明で、電子回路はどのような回路であっても必ず周波数特性を持つということ、すべての波形は様々な周波数と振幅のサイン波の足し合わせで成り立っているということを述べてきました。
電子回路の入力端子には、時間的に変化する電圧や電流の信号が入力され、同様に出力端子からは時間的に変化する電圧や電流の信号が出力されます。このように電圧や電流などが時間的に変化する様子を過渡特性と言います。
さて、これまで説明してきた内容から、周波数特性と過渡特性の間には密接な関係があることを想像して頂けると思います。図8 は、ローパス特性を持つ電子回路 A に矩形波を入力した様子を表しています。

図8. 矩形波入力に対する出力波形
ローパス特性については既に説明していますが、図3 (a) のようなに周波数が低い領域では信号が衰えずに出力され、周波数が高くなるほど出力される信号が減衰していく周波数特性です。
また、矩形波は式(1) で表されますが、図5 のように式(1) の k の値が大きいほどきれいな矩形波に近づきます。k の値が大きいほど高い周波数成分を含むことを意味しています。矩形波は時間的な変化が急峻な部分を持つ波形ですが、一般的に急峻な部分は高い周波数成分により形成されます。
もう一度、図5 の波形を見てみると k の値が小さいほど波形が鈍って(なまって)おり、k の値が大きいほど波形の急峻な部分が形成されていく様子が分かると思います。
よって、図8 のようにローパス特性を持つ電子回路に矩形波を入力した場合、出力に現れる波形は鈍った(なまった)ものとなります。これは回路のローパス特性により、高い周波数成分が除去されるためです。
このように、周波数特性と過渡特性の間には密接な関係があることを理解して頂けたかと思います。ここまでは感覚的な説明をしてきましたが、周波数特性と過渡特性の両方の特性を表す数式があります。それが伝達関数です。
電子回路の特性は、伝達関数と呼ばれる数式で表されます。この伝達関数については、詳しくは当サイトの「第3章 制御工学 入門」で説明しています。伝達関数は複素数の関数で、この伝達関数から周波数特性や過渡特性を求めることができます。
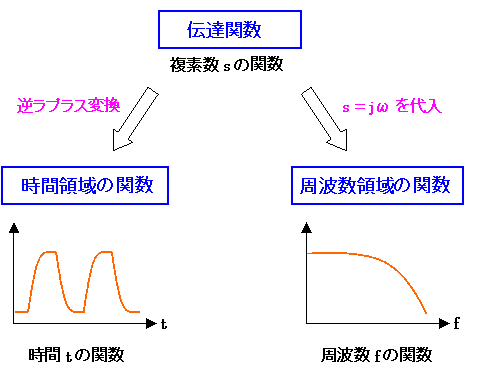
図9. 時間の関数と周波数の関数
もっと正確に周波数特性と過渡特性について理解するには、「3-1. 制御工学(制御理論)の基礎」や「3-6. 周波数特性とボード線図」をご覧ください。