1. 制御工学（制御理論）とは

冒頭で、「制御工学（制御理論）を学ぶこと」=「伝達関数を理解すること」と述べました。伝達関数は F(s) というように 複素数 s の関数で表されます。複素数とは、実数と虚数を含んだ数です。虚数とは 2乗して -1 となる数のことで、実際には存在しない数です。-1 のルートが虚数ということになります。

私たちが「入出力の関係を表す関数」といって直感的に理解しやすいのは、y(t) = f(t) × x(t) というような時間 t の関数です。しかし伝達関数は、”時間領域”ではなく”s領域”（s空間）の関数なのです。

制御工学の計算では、時間 t の関数を「ラプラス変換」と呼ばれる手法を用いて複素数 s の式に変換します。そして伝達関数を含む計算を解き、システムの出力特性を求めます。そして今度は「逆ラプラス変換」という手法を用いて、 s領域（s空間）から再び時間領域の式に戻します。制御工学の解析では、以上のような方法を用います。分かりやすく例えるため、図1 の図を使って説明しましょう。

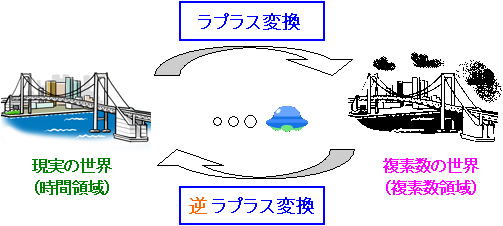
図1. ラプラス変換のイメージ

あるシステムに入力波形を入力し、どのような出力が出てくるのかを調べたいのですが、現実の世界（時間領域）ではなく複素数の世界（複素数領域）に行けば簡単に計算できます。そこで「ラプラス変換」というツール（道具）を使って複素数の世界へ飛んでいきます。

そして、複素数の世界で出力がどうなるか計算します。しかし困ったことに、われわれは複素数の世界にいたままでは、計算結果を理解することができません。なぜなら、その計算結果は複素数 s の関数だからです。なので「逆ラプラス変換」を使い、再び現実の世界（時間領域）に戻ってきます。

こうすることにより計算結果は時間 t の関数になり、システムの出力特性を求めることができるのです。以上が、制御工学の計算の基礎になります。

それにしても制御工学の計算ではなぜ、わざわざ時間領域から複素数領域への変換が必要なのでしょうか？その理由については、「3-5. 伝達関数ってなに？」で述べたいと思います。

2. フィードバック制御

制御工学は別名、フィードバック制御とも言われます。フィードバックとは、制御工学の基礎となる考え方です。フィードバック制御は、出力の一部を入力に帰還（フィードバック）して、出力をある目標値にするための制御のことです。一つ例を挙げると、温度を一定に保つために温度を検出しながら火力を調整するといったことです。

図2 に、簡単なフードバックのイメージを示します。図2 は、入出力システムの伝達関数 H(s) があり、その出力を伝達関数 G(s) のフィードバック要素を使って入力に帰還している様子を表しています。

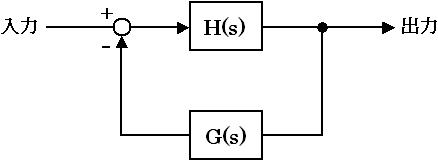
図2. フィードバックのイメージ

フィードバック制御は出力の一部を入力に帰還することにより、安定した出力を得るための仕組みなのですが問題があります。それは制御の仕方を間違えると不安定になるということです。制御工学（制御理論）では、フィードバック制御の安定性の判別を行うことができます。この安定性の判別は、制御工学（制御理論）の特徴の一つです（本サイトでは、安定性の判別方法の説明までは行っていません）。

フィードバック制御のイメージや、なぜシステムが不安定になるのかということについては「3-7. フィードバック制御」で説明しています。

3. 抵抗、容量、コンデンサについて

第3章「制御工学 入門」では、抵抗、容量、コンデンサといった回路素子で構成された回路を使って、入出力特性を説明していきます。そのためまず、これらの回路素子の特徴について説明したいと思います。

まずは「抵抗」という回路素子についてですが、オームの法則というものがあります。電圧を V 、電流を I 、抵抗値を R とすると、 V=R×I と表せます。
この式は、 V と I が時間的に変化する場合においても成り立ちます（電圧 v(t) と電流 i(t) ）。つまり、下式(1) のようになります。

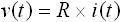
・・・ (1)

次に「容量」という回路素子について説明します。「容量」というより「コンデンサ」といった方が分かるという人もいるでしょう。以下、「容量」で統一します。 図3 (a) は容量のイメージで、容量の両端に電圧 v(t) がかかっている様子を表しています。このとき容量に電荷が蓄えられます。

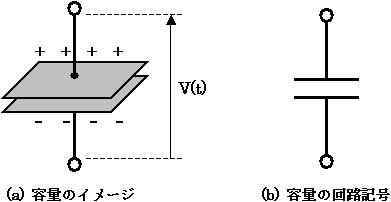
図3. 容量のイメージと回路記号

容量は、電圧が時間的に変化するとそれに比例して電荷も変化するという特徴を持ちます。よって、下式(1) が容量の特徴を表す式ということになります。

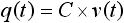
・・・ (2)

q は電荷量、 C は容量値、 v は電圧です。q(t) や v(t) の (t) は時間 t の関数であることを表し、電荷量と電圧は時間的に変化します。

一方、電流とは電荷の時間的な変化であることから下式(2) のように表されます（ i は電流）。

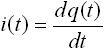
・・・ (3)

よって、式(2) に式(1) を代入すると、容量の電流と電圧の関係式は以下のようになります（式(3) ）。

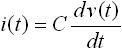
・・・ (4)

式(3) は、容量に電圧をかけたときの電流値について表したものですが、両辺を積分することにより、電流を与えたときの電圧値を表す式に変形できます。下式(4) がその式になります。

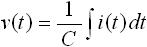
・・・ (5)

以上が容量の特徴です。

最後に、インダクタの特徴について説明します。インダクタは「コイル」ととも言われますが、ここでは「インダクタ」で統一します。図4 (a) はインダクタのイメージで、インダクタに流れる電流 i(t) の変化に伴い逆起電力が発生する様子を表しています。

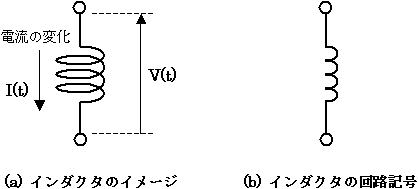
図4. インダクタのイメージと回路記号

インダクタは、電流の時間的な変化量（電流を時間で微分した値）に比例して、逆起電力が発生するという特徴を持ちます。よって、下式(5) がインダクタの特徴を表す式ということになります。

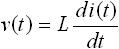
・・・ (6)

ここで L はインダクタンスと呼ばれる定数です。式(5) は、インダクタに電流を流したときの電圧値について表したものですが、両辺を積分することにより、電圧を与えたときの電流値を表す式に変形できます。下式(6) がその式になります。

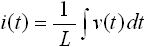
・・・ (7)

以上がインダクタの特徴です。

それでは次節「3-2. ラプラス変換」で、ラプラス変換について説明します。