電子回路設計の基礎 > 3-2. ラプラス変換
ラプラス変換
このページでは、制御工学(制御理論)の計算で用いるラプラス変換について説明します。ラプラス変換を用いる計算では、ラプラス変換表を使うと便利です。
1. ラプラス変換とは
前節、「3-1. 制御工学(制御理論)の基礎」で、制御工学の計算ではラプラス変換を使って時間領域 t から複素数領域 s (s空間)に変換すると述べました。ラプラス変換の公式は、後ほど説明しますが、積分を含むため計算が少し厄介です。「積分」と聞いただけで、嫌気がさす方もいるでしょう。
しかしラプラス変換表を使えば、わざわざラプラス変換の計算をする必要がなくなるので非常に便利です。表1 にラプラス変換表を示します。 f(t) の欄の関数は原関数と呼ばれ、そのラプラス変換を F(s) の欄に示しています。
表1. ラプラス変換表
| f(t) | F(s) | 備考 | |
| 1 | 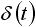 |
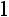 |
δ(t) はインパルス関数(デルタ関数) インパルス関数の詳細は、「3-5. 伝達関数ってなに?」で説明しています。 |
| 2 | 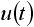 |
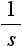 |
u(t) はステップ関数(ヘビサイド関数) t<0で 0 、t≧0で 1 となる関数です。 |
| 3 | 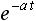 |
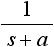 |
- |
| 4 | 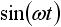 |
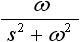 |
- |
| 5 | 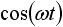 |
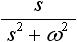 |
- |
| 6 | 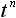 |
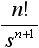 |
- |
| 7 | 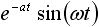 |
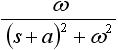 |
- |
| 8 | 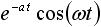 |
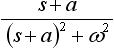 |
- |
| 9 | 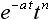 |
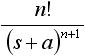 |
- |
| 10 | 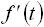 |
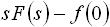 |
f(t) の微分 f(t) は t の任意に関数、 F(s) は s の任意の関数です。 |
| 11 | 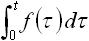 |
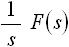 |
f(t) の積分 f(τ) は τ の任意に関数、 F(s) は s の任意の関数です。 |
ここで、表1 の1番目と2番目の関数について少し説明をしておきます。1番目の δ(t) はインパルス関数(または、デルタ関数)と呼ばれ、図1 (a) のように t=0 のときのみ ∞ となります( t=0 以外は 0 となります)。このインパルス関数は特殊で、後ほど「3-5. 伝達関数ってなに?」で説明することにします。
表1 の2番目の u(t) はステップ関数(または、ヘビサイド関数)と呼ばれ、図1 (b) のような t<0 で 0 、 t≧0 で 1 となる関数です。
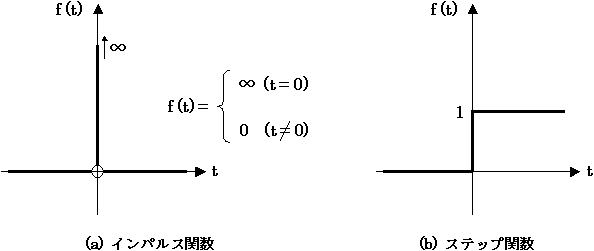
図1. インパルス関数(デルタ関数) と ステップ関数(ヘビサイド関数)
それでは次に、「3-1. 制御工学(制御理論)の基礎」で説明した抵抗、容量、インダクタの式に関してラプラス変換を行い、s関数に変換します。実際に、ラプラス変換表を使ってみましょう。
◆ おすすめの本 - 演習で学ぶ基礎制御工学
↓↓ 内容の一部を見ることができます ↓↓
- 演習を通して、制御工学の内容を理解できる。
- 多くの具体例(電気回路など)を挙げて、伝達関数を導出しているので実践で役に立つ。
- いろいろな伝達関数について周波数応答(周波数特性)と時間関数(過渡特性)を求めており、周波数特性を見て過渡特性の概要を思い浮かべることが出来るように工夫されている。
- ラプラス変換とラプラス逆変換の説明
- 伝達関数の説明と導出方法の説明
- 周波数特性と過渡特性の説明
- システムの安定判別法について
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
2. 抵抗、容量、インダクタのラプラス変換
(1) 抵抗のラプラス変換
まずは、抵抗のラプラス変換です。前節「3-1. 制御工学(制御理論)の基礎」より、電流と電圧の関係は下式(1) で表されます。
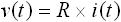
・・・ (1)
v(t) と i(t) は任意の時間関数であるため、ラプラス変換すると V(s) 、 I(s) のように任意の s関数となります。また、抵抗値 R は時間 t に依存しない定数であるため、式(1) のラプラス変換は下式(2) のようになります。
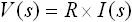
・・・ (2)
式(2) は入力電流 I(s) に対する出力電圧 V(s) の式のようになっていますが、式(1) を変形して、入力電圧 V(s) に対する出力電流 I(s) の式は下式(3) のように求まります。
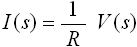
・・・ (3)
以上が、抵抗のラプラス変換の説明です。
(2) 容量(コンデンサ)のラプラス変換
次に、容量(コンデンサ)のラプラス変換です。前節より、容量の電圧 v(t) と電流 i(t) の関係式下式(4) , (5) と表されます。
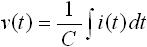
・・・ (4)
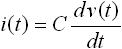
・・・ (5)
式(4) は入力電流 i(t) に対する出力電圧 v(t) の式のです。これを、「表1. ラプラス変換表」の11番目を使って積分のラプラス変換を行うと、下式(6) のように変換されます。
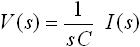
・・・ (6)
一方、式(6) は入力電圧 v(t) に対する出力電流 i(t) の式のです。これを、「表1. ラプラス変換表」の10番目を使って微分のラプラス変換を行うと、下式(7) のように変換されます。
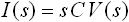
・・・ (7)
以上が、容量(コンデンサ)のラプラス変換の説明です。
(3) インダクタ(コイル)のラプラス変換
次に、インダクタ(コイル)のラプラス変換です。前節より、インダクタの電圧 v(t) と電流 i(t) の関係式下式(8) , (9) と表されます。
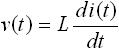
・・・ (8)
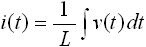
・・・ (9)
式(8) は入力電流 i(t) に対する出力電圧 v(t) の式のです。これを、「表1. ラプラス変換表」の10番目を使って微分のラプラス変換を行うと、下式(10) のように変換されます。
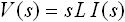
・・・ (10)
一方、式(9) は入力電圧 v(t) に対する出力電流 i(t) の式のです。これを、「表1. ラプラス変換表」の11番目を使って積分のラプラス変換を行うと、下式(11) のように変換されます。
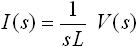
・・・ (11)
以上が、インダクタ(コイル)のラプラス変換の説明です。
制御理論の計算では、「ラプラス変換」を使って時間領域から複素数領域に変換し、「逆ラプラス変換」を使って時間領域に戻します。このラプラス変換、逆ラプラス変換の公式は積分を含んだ式で、実際に計算するのは少し手間を要します。そこで、以下に示すラプラス変換表を使うと非常に便利です。
3. ラプラス変換の計算
まず、ラプラス変換の定義・公式について説明します。時間領域 0 ~ ∞ で定義される関数を f(t) とし、そのラプラス変換を F(s) とするとラプラス変換は下式(12) のように与えられます。
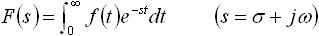
・・・ (12)
s は複素数で実数 σ と虚数 jω から成ります。一方、逆ラプラス変換は下式で与えられる。
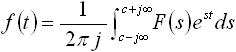
・・・ (13)
制御理論の計算では、「ラプラス変換」を使って時間領域から複素数領域に変換し、「逆ラプラス変換」を使って時間領域に戻します。このラプラス変換、逆ラプラス変換の公式は積分を含んだ式で、実際に計算するのは少し手間を要します。そこで、以下に示すラプラス変換表を使うと非常に便利です。