1. 抵抗分圧回路の動作

抵抗分圧は、電気回路や電子回路の設計でよく利用される手法です。図1 のように、電源電圧 Vcc は抵抗 R1 と R2 によって電圧が分割され、その電圧が Vout に現れるため「抵抗分圧」と呼ばれます。

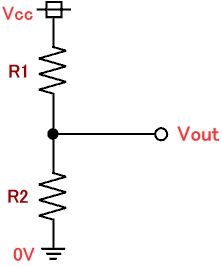
図1. 抵抗分圧 (1)

抵抗 R1 と R2 の直列に接続された2つの抵抗が電源 Vcc とグランド 0V の間にある場合、Vout の電圧は式(1) で表されます。

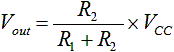
・・・ (1)

この式(1) の法則を「抵抗の分圧則」と言います。

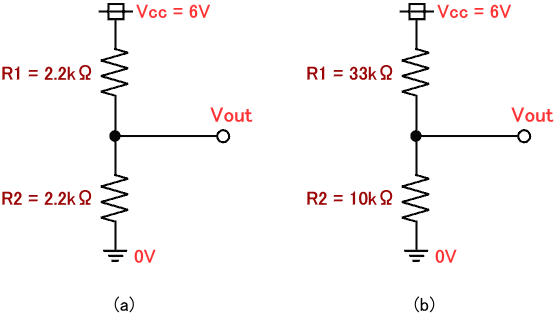
図2. 抵抗分圧 (2)

例えば、図2 (a) のように Vcc=6V で R1 = 2.2 kΩ、R2 = 2.2 kΩであれば出力電圧 Vout は式(2) のように 3.0 V となります。

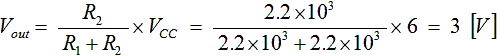
・・・ (2)

ちなみに、R1 と R2 が 2.2kΩでなくても R1 = R2 の場合、抵抗値がどのような値であっても Vout の値は電源 Vcc の半分の値になります。

図2 (a) のように、同じ抵抗を使って電源電圧 Vcc の半分の値（Vcc/2）を得る方法は、電子回路の設計でよく用いられる手法です。覚えておくと便利です。

当然ですが、抵抗値の選び方次第で様々な電圧を作ることもできます。例えば図2 (b) のように Vcc=6V で R1 = 33 kΩ、R2 = 10 kΩとした場合、出力電圧 Vout は式(3) のように 1.395 V となります。

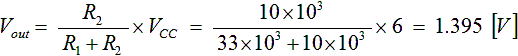
・・・ (3)

それでは次に、ちょっと複雑になりますが図3 (a) の回路の出力電圧 Vout が何 V になるか考えてみましょう。R1 , R2 , R3 はすべて同じ抵抗値です。

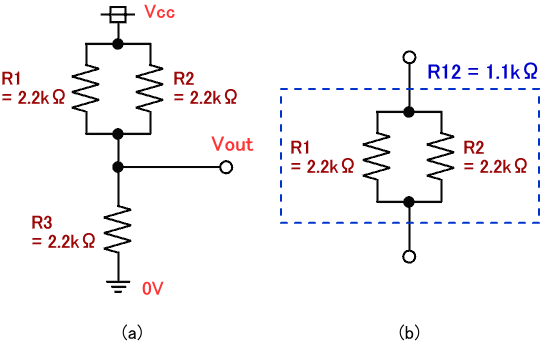
図3. 抵抗分圧 (3)

図3 (a) の回路ですが、まず同図 (b) のように R1 と R2 を1つの抵抗 R12 と考えてみましょう。そうすれば、出力電圧 Vout は式(1) と同様に下式のように求まります。

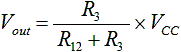
・・・ (4)

一方、抵抗 R1 と R2 は Vcc - Vout間に並列に接続されています。並列に接続された抵抗の合成抵抗 R12 は下式のようになります。

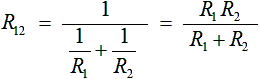
・・・ (5)

式(5) に R1 = R2 = 2.2kΩ を代入すると R12 = 1.1kΩという結果を得ます。抵抗を並列に接続した場合、抵抗値が何であれ R1 = R2 であれば、合成抵抗の値は半分の値になります。

R12 = 1.1kΩ、R3 = 2.2kΩを式(4) に代入することで、図3 (a) の回路の出力電圧 Vout が求まります。計算してみると Vout は下式のように求まります。

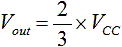
・・・ (6)

図3 (a) の回路は、R1 , R2 , R3 が同じ値であれば抵抗値に寄らず電源電圧 Vcc の3分の2の値（2/3×Vcc）となるという特徴を持ちます。

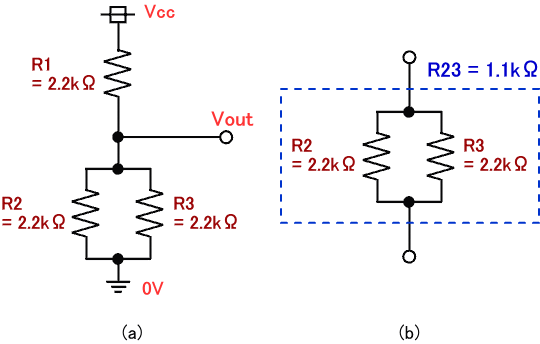
図4. 抵抗分圧 (4)

今度は図4 (a) の回路について、図3 と同様に考えてみましょう。図4 (a) の回路ですが、まず同図 (b) のように R2 と R3 を1つの抵抗 R23 とした場合、出力電圧 Vout は式(1) と同様に下式のように求まります。

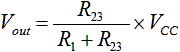
・・・ (7)

一方、抵抗 R2 と R3 は Vout - 0V間に並列に接続されています。並列に接続された抵抗の合成抵抗 R23 は下式のようになります。

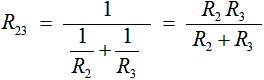
・・・ (8)

式(8) についても R2 = R3 であれば、合成抵抗 R23 は半分の値になります。つまり R23 = 1.1kΩです。

R1 = 2.2kΩ、R23 = 1.1kΩを式(7) に代入することで、図4 (a) の回路の出力電圧 Vout が求まります。計算してみると Vout は下式のように求まります。

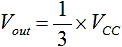
・・・ (9)

図4 (a) の回路は、R1 , R2 , R3 が同じ値であれば抵抗値に寄らず電源電圧 Vcc の3分の1の値（1/3×Vcc）となるという特徴を持ちます。

図3 (a) および図4 (a) で電源電圧 Vcc=6V の場合、R1 = R2 = R3 であれば出力電圧 Vout は図3 (a) が 4V、図4 (a) が 2V となります。

さて、次は実際に抵抗分圧回路をブレッドボード上に構成してみましょう。

2. 抵抗分圧回路を作る

「1. 抵抗分圧回路の動作」で説明した回路を、ブレッドボード上に構成したいと思います。図2 (a)、図3 (a)、図4 (a) の回路を実際に作ってみましょう。図5 に再度回路図をまとめます。

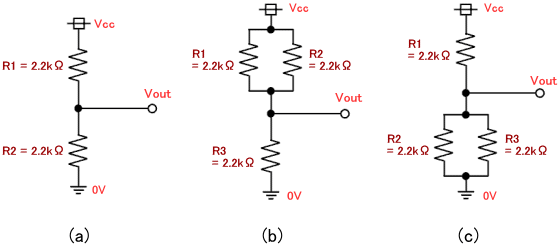
図5. 様々な抵抗分圧回路の回路図

回路図だけ見ながら構成できる方は、ぜひ挑戦してください。回路図だけでは心配な方は図6 および図7 の写真を参考にしてください。

図6. 抵抗分圧回路のブレッドボード上の構成図 (1)

上図の左の写真は、電源となる乾電池をブレッドボードに接続した様子です。ブレッドボードの＋部分に乾電池の＋端子を接続し、ブレッドボードの－部分に乾電池の－端子を接続します。図6 の右の写真は、図5 (a) の抵抗分圧回路を構成した例です。

ブレッドボード上に回路を構成したら、デジタルマルチメータ（テスター）で実際に電圧を測定してみましょう。測定方法については、次の「3. 抵抗分圧回路を測定する」に記しています。

図7. 抵抗分圧回路のブレッドボード上の構成図 (2)

図7 の左の写真は図5 (b) の抵抗分圧回路、図7 の右の写真は図5 (c) の抵抗分圧回路をブレッドボード上に構成した例です。

ブレッドボード上の構成が完了したら、実際に電圧を測定しながら数式で求めた結果と同じになるか確認してみましょう。

3. 抵抗分圧回路を測定する

ブレッドボード上に回路を構成したら、まず始めに電源電圧 Vcc の電圧を測定しましょう。なぜかと言うと Vcc は正確に 6V ではないためです。電源電圧は単三電池（1.5V）4つを直列につないでいるのですが、電池の電圧が 1.5V ちょうどではないのです。そのため Vcc は 6V ちょうどにならないのです。

私が測定したときには Vcc = 6.23 V でした。測定の様子を図8 に掲載しています。

図8. 電源電圧測定の様子

測定器は「デジタル・マルチメータ」を使用しています。デジタル・マルチメータについては、実践編「1-3. 必要な工具・測定器」を参考にしてください。

図5 (a) の回路の Vout電圧は、数式から求めた結果 Vcc の 2分の1 の値でした。よって理論的には Vcc = 6.23 V の半分の値である 3.115 V が Vout の電圧となるはずです。実際にはどうなるでしょうか？電圧を測定している様子を図9 に示します。

図9. 抵抗分圧回路の電圧測定 (1)

上の写真の通り 3.10 V という結果で、ほぼ数式から求めた結果と一致しました。

続いて図5 (b) と図5 (c) の回路の電圧を測定してみましょう。数式から求めた結果は図5 (b) が Vcc の 3分の2、図5 (c) が Vcc の 3分の1 でした。Vcc = 6.23 V でしたので、理論的にはそれぞれ 4.153 V と 2.077 V になるはずです。

図10. 抵抗分圧回路の電圧測定 (2)

図11. 抵抗分圧回路の電圧測定 (3)

上の写真が電圧測定の様子で、それぞれ 4.15 V と 2.07 V になりました。これもほぼ数式から求めた結果と一致しました。

実際の測定値と計算値がほぼ等しければ、正しく回路を構成できたことになります。（抵抗値にはばらつきが存在するため、測定値と計算値がぴったし合わないことがあります。）

もし、値が大きく違う場合は、ブレッドボード上に構成した回路や計算結果が正しいか確認してください。

それでは次のページ「3-3. コンパレータ（比較器）」で、コンパレータ（比較器）について学んでいきましょう。