電子回路設計の基礎 > 3-6. 周波数特性とボード線図
周波数特性とボード線図
これまで説明してきた内容は、時間領域とs領域(s空間)の関係についてです。制御工学(制御理論)において、もう一つ重要なものとして周波数領域とs領域(s空間)の関係があります。このページでは伝達関数から周波数特性を導出する方法と、その周波数特性を視覚的に示したボード線図について説明します。
1. 伝達関数と周波数特性の関係
「3-4. 伝達関数の求め方」で、伝達関数を求める方法を説明しました。その伝達関数を逆ラプラス変換することで、時間領域の式に変換することができることも既に述べました。
このページで説明する内容は、伝達関数と周波数特性の関係です。伝達関数は、周波数領域へ変換することが可能です。その方法はとても簡単で、複素数 s を jω に置き換えるだけです。つまり、伝達関数の s に s=jω を代入するだけでいいのです。
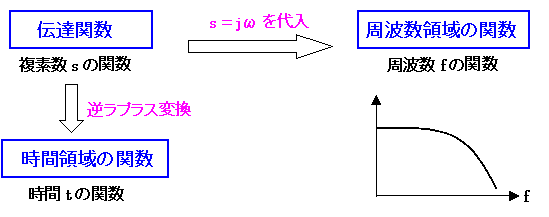
図1. 伝達関数からの変換
図1 に、伝達関数から時間領域 t への変換と周波数領域 f への変換の様子を示しています。時間領域の関数を求めるには逆ラプラス変換を行えばよく、周波数領域の関数は s=jω を代入すれば求めることができます。
ここで j は虚数と呼ばれるもので、2乗して -1 となる数のことです。また、 ω は角速度(または角周波数ともいう)と呼ばれ、周波数 f とは ω=2π×f の関係式で表されます。
たとえば下式(1) のように、伝達関数 sY/(1+sX) に s=jω を代入すると jωY/(1+jωX) を得ます。
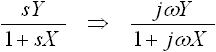
・・・ (1)
つまり、任意の周波数 f (f=ω/2π)のサイン波に対する挙動を上式は表しています。虚数 j を使ってなぜサイン波に対する挙動を表すことができるかについては、「第2章 電気回路 入門」の「2-3. 交流回路と複素数」で述べていますので参照してください。
この周波数特性のことを、制御工学では「周波数応答」といいます。また周波数応答は、横軸を周波数 f として視覚的にグラフで表すことができます。後ほど説明しますが、このグラフを「ボード線図」といいます。
◆ おすすめの本 - 演習で学ぶ基礎制御工学
↓↓ 内容の一部を見ることができます ↓↓
- 演習を通して、制御工学の内容を理解できる。
- 多くの具体例(電気回路など)を挙げて、伝達関数を導出しているので実践で役に立つ。
- いろいろな伝達関数について周波数応答(周波数特性)と時間関数(過渡特性)を求めており、周波数特性を見て過渡特性の概要を思い浮かべることが出来るように工夫されている。
- ラプラス変換とラプラス逆変換の説明
- 伝達関数の説明と導出方法の説明
- 周波数特性と過渡特性の説明
- システムの安定判別法について
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
2. 周波数特性の例(ローパス特性)
それでは実際に図2 の回路を例に挙げ、周波数特性(周波数応答)を求めてみましょう。ここでは、周波数特性を表すのに複素数を使います。周波数特性と複素数の関係を理解するためには「2-3. 交流回路と複素数」を参照してください。
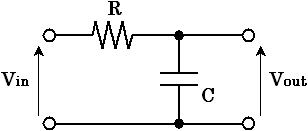
図2. 抵抗とコンデンサで構成された回路
図2 は抵抗 R とコンデンサ C で構成されており、入力電圧を Vin 、出力電圧を Vout とすると伝達関数 Vout/Vin は下式(2) のように求まります。
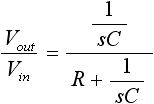
・・・ (2)
伝達関数の求め方は、「3-4. 伝達関数の求め方」を参照してください。また、式(2) は「分圧則」を用いて求めています(「2-5. 交流回路(交流理論)の基礎」の「4. 分圧則、分流則」を参照してください)。式(2) の右辺に sC/sC を掛けると、最終的に伝達関数は下式(3) になります。

・・・ (3)
さて、ここで図2 の回路の周波数特性を得るために s=jω を代入すると下式(4) を得ます。
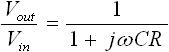
・・・ (4)
さらに、式(4) を有理化すると下式(5) を得ます(有理化については、「2-5. 交流回路(交流理論)の基礎」の「3. 複素数の有理化」を参照してください)。
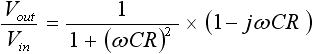
・・・ (5)
横軸を実数、縦軸を虚数として式(5) を図に表すと、図3 のようになります。
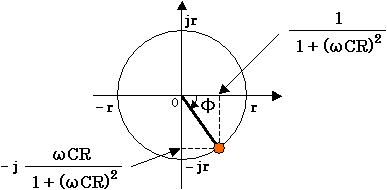
図3. 横軸を実数、縦軸を虚数として表した図
式(5) や図3 の意味ですが、入力にある周波数の正弦波(サイン波)を入力したときに、出力の正弦波の振幅や位相がどのように変化するかということを示しています。具体的には図4 の通りです。図4 (a) のように振幅 1 の正弦波を入力したときの出力が、同図 (b) のように振幅と位相が変化することを表しています。
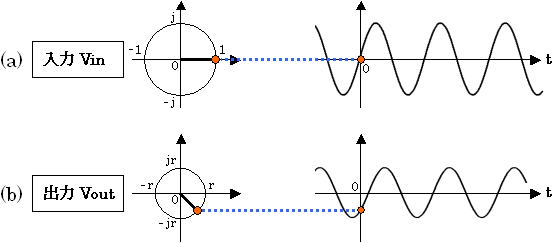
図4. 入力と出力の位相と振幅の関係
振幅を数式で表すと式(6) のように表すことができます。
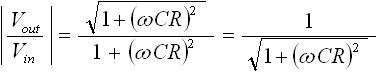
・・・ (6)
また、位相のずれを数式で表すと式(7) のように表すことができます。

・・・ (7)
それでは次に、式(6) 、式(7) の周波数特性(周波数応答)を視覚的に分かりやすいようにグラフで表した「ボード線図」について説明します。
3. ボード線図
ここでは、周波数特性(周波数応答)の特徴をグラフで表現する「ボード線図」について説明します。ボード線図は「ゲイン特性」と「位相特性」の二種類あり、それぞれ以下のような特徴を持ちます。
(1) ゲイン特性
- 角周波数 ω を横軸とし、角周波数は対数目盛りでとる。
- 振幅を r とすると 20×log r を縦軸にとる(単位は dB )。
(2) 位相特性
- 角周波数 ω を横軸とし、角周波数は対数目盛りでとる。
- 位相のずれ Φ を縦軸にとる(単位は 度 )。
それでは、「2. 周波数特性の例 (ローパス特性)」で説明した回路のボード線図がどのようなものなのか見てみましょう。振幅の式である式(6) はゲイン特性の式で、位相の式である式(7) は位相特性の式です。図5 は式(6) のゲイン特性を示したものです。
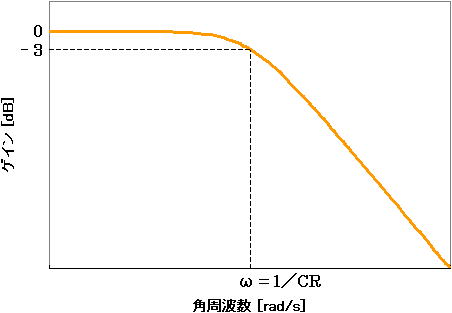
図5. ボード線図のゲイン特性
図6 は式(7) の位相特性を示したものです。
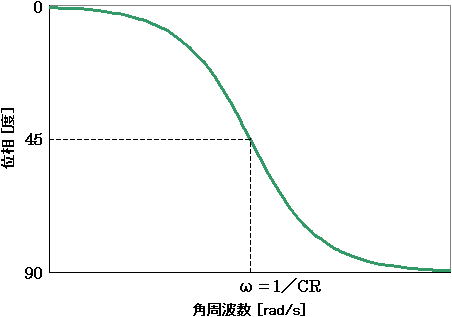
図6. ボード線図の位相特性
図5 、図6 の横軸を周波数 f=ω/(2π) で置き換えることも可能です。なお、ゲインが 3 dB 落ちたところの周波数 ω = 1/(CR) は伝達関数の”極”にあたり、カットオフ周波数と呼ばれます(周波数 : f = 1/(2πCR) 。)
以上が、周波数特性(周波数応答)とボード線図(ゲイン特性と位相特性)の説明になります。