1. RC回路の動作

図1 が前ページ「3-4. 矩形波（方形波）発生回路」で作成した矩形波（方形波）発生回路の回路図です。

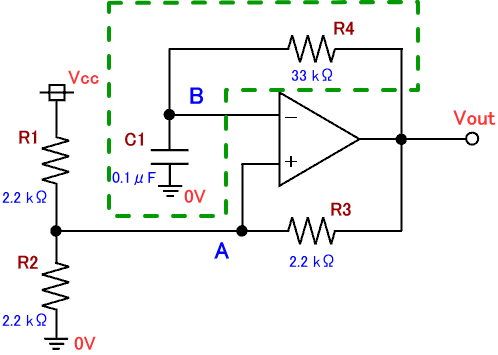
図1. 矩形波（方形波）発生回路

図1 の緑の点線で囲った部分がRC回路です。このRC回路が、矩形波（方形波）発生回路の周波数を決める部分です。RC回路は抵抗とコンデンサで構成された単純な回路ですが、電子回路ではよく使われる回路です。

改めて RC回路のみを図2 に示します。V1 を RC回路の入力端子、V2 を出力端子とします。

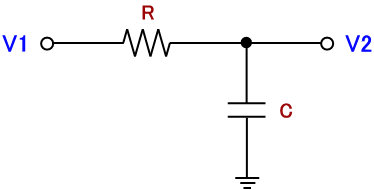
図2. RC回路

図1 の Vout端子はコンパレータの出力にあたり、コンパレータの2つの入力端子の大小関係により 0V になったり Vcc電圧になったりします。大小関係が変わるとすぐに、0V → Vcc や Vcc → 0V へと瞬間的に変化することは前ページまでに説明した通りです。

よって RC回路にとっては、入力端子（図2 の V1 ）に図3 のような波形が入力されるということになります。（赤線が波形です。）

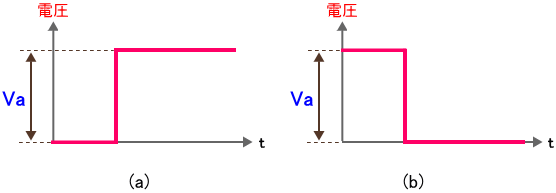
図3. RC回路に入力される波形

図3 (a) が 0V → Va に変化する波形で、同図 (b) が Va → 0V に変化する波形です。（ここで、Va は波形の振幅を表します。）一方、出力である図2 の V2 の電圧はどのような波形になるかと言うと、図3 (a) の入力に対しては式 (1) で表されます。

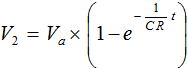
・・・ (1)

また、図3 (b) の入力に対して、出力は式 (2) で表されます。

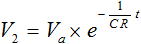
・・・ (2)

式 (1) および式 (2) を分かりやすく図示したものが図4 になります。図4 (a) の上の図が入力で、それに対する出力である式 (1) の波形が下の図です。同様に同図 (b) の上の図が入力で、それに対する出力である式 (2) の波形が下の図です。

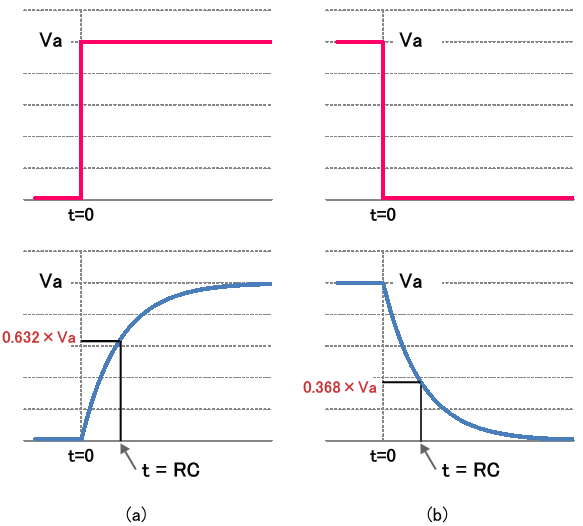
図4. RC回路から出力される波形

まず、図4 (a) から説明します。式 (1) を見ると分かるように時間 t が R×C となったとき、電圧の値は 0.632 × Vcc となります。つまり、図2 の入力 V1 が瞬間的に 0V → Va になるのに対して、出力 V2 は時間 t = R×C 秒後に Vcc 電圧の 63.2% まで立ち上がることを意味します。

次に図4 (b) ですが、式 (2) を見ると分かるように時間 t が R×C となったとき、電圧の値は 0.368 × Vcc となります。つまり、図2 の入力 V1 が瞬間的に Vcc → 0V になるのに対して、出力 V2 は時間 t = R×C 秒後に Vcc 電圧から見て 63.2% まで 0V に近づくことを意味します。

この R×C を時定数といい、一般的に式 (3) のように τ（タウ）で表されます。

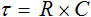
・・・ (3)

時定数 τ の値が小さいと出力 V2 の立ち上がり（立ち下がり）は速く、τ の値が大きいと V2 の立ち上がり（立ち下がり）は遅くなります。図5 に、時定数 τ の値を倍および半分にした時の出力 V2 の様子を示します。

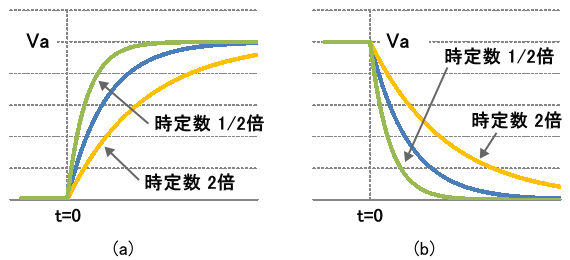
図5. 時定数 τ の値に対するRC回路の出力波形

図5 (a) は立ち上がりの様子で、時定数を半分にした時の波形が緑色、時定数を2倍にした時の波形が黄色です。同様に同図 (b) は立ち下がりの様子で、時定数を半分にした時の波形が緑色、時定数を2倍にした時の波形が黄色です。

それでは次に、これまでの時定数の説明を踏まえて図1 の R と C の値を変えた時にどのようになるのか実験してみましょう。

2. RC回路と矩形波発生回路の実験

前のページ「3-4. 矩形波（方形波）発生回路」で説明しましたが、矩形波発生回路（図1）の A点、B点および Vout の電圧の時間変化は図6 のようになります。

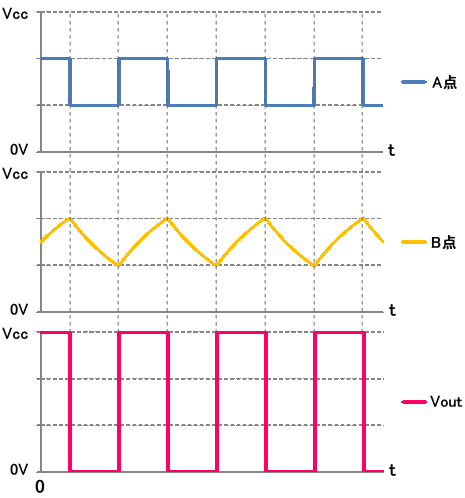
図6. 矩形波（方形波）発生回路の動作

B点の動作に関しては、Vout の電圧の変化に対して遅れるように変化することも既に述べました。

矩形波（方形波）発生回路の Vout の電圧は、瞬間的に 0V → Vcc や Vcc → 0V に変化します。その電圧を入力として、RC回路の出力が B点に当たります。

R×C の値が小さいと B点の変化の動作は早くなります。一方、R×C の値が大きいと B点の変化の動作は遅くなります。それでは、早速、実験してみましょう。

図1 の R と C の値はそれぞれ R = 33 kΩ、C = 0.1 μF です。この時の Vout の波形を図7 に示します。

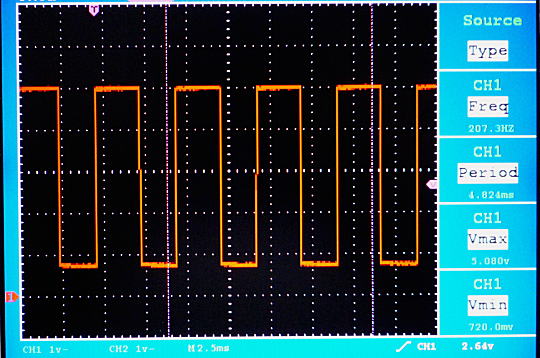
図7. オシロスコープの画像 (1)

上図はオシロスコープの画像で、周波数を確認すると 207.3 Hz となっています。

まずは抵抗 R の値を半分にしてみましょう。抵抗値の値を半分にするために 33 kΩ の抵抗をもう一本追加します。同じ抵抗値のものを並列にすると、図8 のように抵抗値は半分になります。

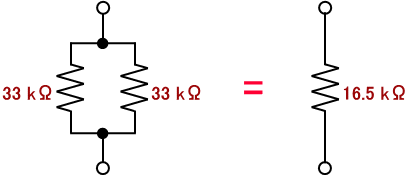
図8. 並列接続した抵抗

抵抗値の値が半分になると時定数 τ = R×C の値も半分になります。この時の Vout の波形を図9 に示します。

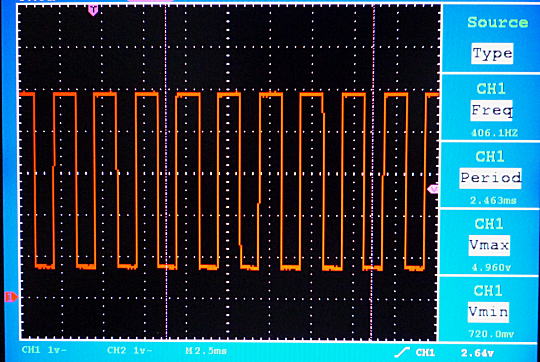
図9. オシロスコープの画像 (2)

上図のオシロスコープの画像を確認すると周波数が 406.1 Hz となっており、約倍の周波数となっています。

次に容量 C の値を倍にしてみましょう。容量値の値を倍にするために 0.1 μF のコンデンサをもう一本追加します。同じ容量値のものを並列にすると、図10 のように容量値は倍になります。

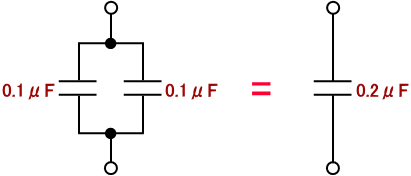
図10. 並列接続したコンデンサ

容量値の値が倍になると時定数 τ = R×C の値も倍になります。この時の Vout の波形を図11 に示します。

図11. オシロスコープの画像 (3)

上図のオシロスコープの画像を確認すると周波数が 105.3 Hz となっており、約半分の周波数となっています。

以上が、RC回路と矩形波（方形波）発生回路の実験です。RC回路の動作を理解できたでしょうか？それでは次のページ「3-6. 矩形波（方形波）発生回路の理論的な理解」で、矩形波（方形波）発生回路の周波数の理論式を求めてみたいと思います。