電子回路設計の基礎 > 2-5. 交流回路(交流理論)の基礎
交流回路(交流理論)の基礎
これまで電気回路について説明してきましたが、このページでようやく「交流回路(交流理論)の基礎」というタイトルを付けることができました。実際には、前節「2-4. インピーダンスとアドミタンス」を理解できれば、交流回路の基礎の半分は理解できていることになると思います。
このページ「交流回路(交流理論)の基礎」では、「2-1. 電気回路の基礎」で直流回路をパズルのように解いたように、交流回路をパズルのように解く方法について説明していきます。
1. インピーダンス、アドミタンス計算のルール
前節「2-4. インピーダンスとアドミタンス」で抵抗、インダクタ、容量のインピーダンスとアドミタンスが表1 のようになると述べました。インピーダンスとアドミタンスの関係は常に逆数の関係にありますが、これは非常に重要な特徴です。
表1. インピーダンスとアドミタンス
| インピーダンス Z | アドミタンス Y | |
| 抵抗 | R | 1/R (= G ) |
| インダクタ | jωL | 1/(jωL) |
| コンデンサ | 1/(jωC) | jωC |
そして、入力を交流電流 I とし、そのときの出力電圧を V とするとインピーダンス Z を用いて下式(1) のように与えられます。
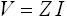
・・・ (1)
一方、入力を交流電圧 V とし、そのときの出力電流を I とするとアドミタンス Y を用いて下式(2) のように与えられます。
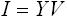
・・・ (2)
ここまでは、前節で述べたことです。新たなルールとして、合成インピーダンスと合成アドミタンスの求め方があります。抵抗、インダクタ、容量が直列に接続されているときはそれぞれのインピーダンスを足し合わせ、一方、並列に接続されたときはアドミタンスを足し合わせます。
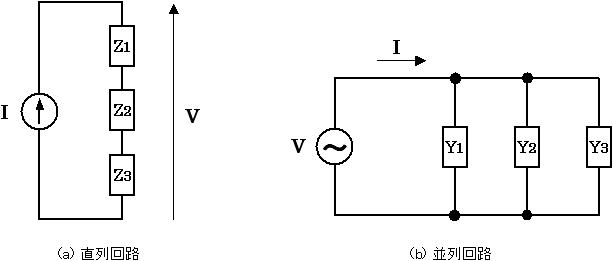
図1. 交流回路
図1 (a) は、抵抗、インダクタ、容量といった素子が直列に接続されている様子を表しており、それぞれのインピーダンスを Z1 , Z2 , Z3 とするならば合成インピーダンス Ztotal は Ztotal = Z1+Z2+Z3 と求まります。この回路に交流電流 I を流したときの回路の両端にかかる電圧は、式(1) より以下のようになります。
V = (Z1 + Z2 + Z3) × I ・・・ (3)
また、図1 (b) は、回路素子が並列に接続されている様子を表しており、それぞれのアドミタンスを Y1 , Y2 , Y3 とするならば、合成アドミタンス Ytotal は Ytotal = Y1+Y2+Y3 と求まります。この回路に交流電圧 V をかけたときに回路に流れる全電流は、式(2) より以下のようになります。
I = (Y1 + Y2 + Y3) × V ・・・ (4)
さて、ここで交流回路をパズルのように解くための「決まり事」について説明します。「決まり事」は以下の通りです。
決まり事(1) ・・・ 求めるものが電圧か電流かで合成インピーダンス Ztotal か合成アドミタンス Ytotal のどちらを求めるか決める。
・ 求める値が電圧の場合 : V = Ztotal × I の合成インピーダンス Ztotal を求める。
・ 求める値が電流の場合 : I = Ytotal × V の合成アドミタンス Ytotal を求める。
決まり事(2) ・・・ 直列接続なら合成インピーダンス、並列接続なら合成アドミタンスを求める。
・ 抵抗が直列接続されている場合 : 合成インピーダンス Ztotal = Z1+Z2+Z3+・・・ を求める。
・ 抵抗が並列接続されている場合 : 合成アドミタンス Ytotal = Y1+Y2+Y3+・・・ を求める。
決まり事(3) ・・・ インピーダンス Z とアドミタンス Y の変換は、お互いを逆数にする。( Z = 1/Y , Y = 1/Z )
それでは、以上の決まり事を使って実際に回路を計算してみましょう。
2. 交流回路の計算
下図2 の回路は抵抗、インダクタ、容量が直列に接続された回路で、交流電圧 V が与えられます。このとき、抵抗、インダクタ、容量に流れる電流 I を求めてみましょう。
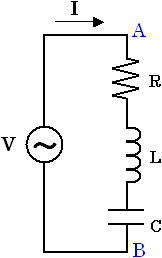
図2. 抵抗、インダクタ、容量で構成された回路
交流電圧 V が与えられており、求めるものは電流 I であるため「 決まり事(1) 」より I = Ytotal × V の Ytotal を求めます。つまり、A点-B点間の合成アドミタンス Ytotal を求めます。
次に、A点-B点間の回路素子 R , L , C に注目します。それぞれ直列に接続されているため、「 決まり事(2) 」よりインピーダンス Ztotal を求めます。 Ztotal は下式(5) のようになります。
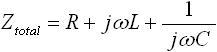
・・・ (5)
ここで、 1/j = -j より式(5) は式(6) のように変形できます。
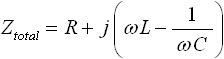
・・・ (6)
さて、始めに「 決まり事(1) 」より、求めるものが電流 I であることから合成アドミタンスを求めると述べました。そこで「 決まり事(3) 」を使って式(6) の合成インピーダンス Ztotal を合成アドミタンスに変換します。合成アドミタンスは下式(7) となります。
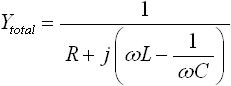
・・・ (7)
よって、 I = Ytotal × V に式(7) を代入することにより、次式(8) を得ることができます。
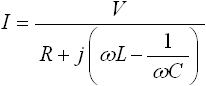
・・・ (8)
ここで「2-3. 交流回路と複素数」で説明した複素数の割り算の特徴を思い出しましょう。複素数 a + jb と c + jd の割り算である ( a + jb )/( c + jd ) の結果は図3 のように、原点からの距離は r1/r2、実軸とのなす角は Φ1 - Φ2 となります。
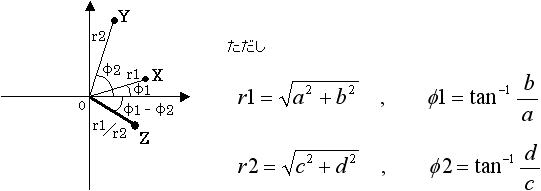
図3. 複素数の割り算
つまり、式(8) の V を V+j0 の複素数と考えると、振幅 I0 と位相のずれ Φ は下式(9) , (10) で求まります。
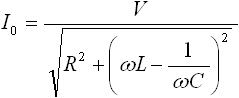
・・・ (9)
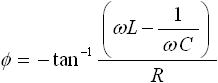
・・・ (10)
図2 の回路についての計算は以上です。
電気回路には、様々な定理や法則が存在します。ざっと挙げてみても、キルヒホフの法則、重ね合わせの理、テブナンの定理、ノートンの定理などなど・・・です。しかし当サイトでは、定理や法則の説明までは行っていません。理解しやすい本を2冊ほど紹介しておきますので、参考にしてみてください。
◆ 計算力を身に付けながら学びたい方へ
↓↓ 内容の一部を見ることができます ↓↓
- 電気回路の演習を解きながら知識を得ることができます。
- 全ページにわたり演習と解説という流れなので、電気回路への理解と実力がしっかりと身に付きます。
- 電気回路の定理や法則を、実際の回路例を参考にしながら理解できます。
- インピーダンスやアドミタンスの計算
- 共振回路、三相交流の説明
- 電気回路の定理や法則を用いた計算
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
それでは最後に、電気回路の計算に必要な手法である「複素数の有理化」や「分圧則、分流則」について説明します。有理化や分圧則、分流則は電気回路の計算でよく使う手法です。
3. 複素数の有理化
複素数の有理化とは、 1/(a+jb) といった形の複素数を c+jd といった形に変換する方法です。 c+jd という形にするためには 1/(a+jb) の分母、分子のそれぞれに a-jb を掛けてやります(虚数部の符号のみを反転してやるとよい jb → -jb )。すると下式(11) のようになります。
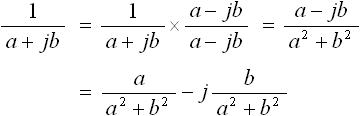
・・・ (11)
この有理化という手法は、図4 のような回路を計算するときに使います。
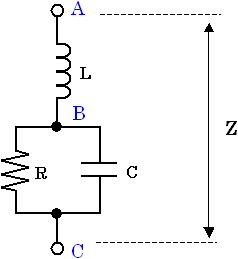
図4. 抵抗、インダクタ、容量で構成された回路 (2)
この回路のB点-C点間のアドミタンス YRC は式(12) のようになるため、A点-C点間のインピーダンス Z は式(13) のようになります( Z = jωL + 1/YRC )。
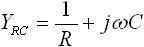
・・・ (12)
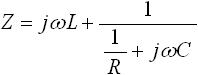
・・・ (13)
この式(13) は、振幅や位相のずれを求めるために a+jb の形にしてやる必要があります。そこで右辺の第2項について有理化を行います(式(14) )。
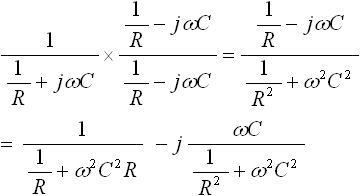
・・・ (14)
すると、式(13) は下式(15) のようになります。
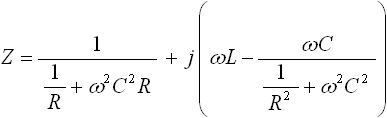
・・・ (15)
以上が、複素数の有理化の説明です。
4. 分圧則、分流則
分圧則、分流則とは、図5 (a) のように電圧 V が与えられたときの各素子にかかる電圧を求めたり、図5 (b) のように電流 I が与えられたときの各素子に流れる電流を求める方法です。
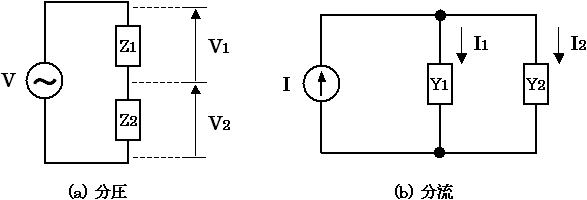
図5. 分圧、分流
図5 (a) は回路素子が直列に接続されており、そこに電圧 V がかかっている様子を表しています。ここで各素子のインピーダンスを Z1 、 Z2 とすると、それぞれの回路素子にかかる電圧は下式(16) の式で与えられます。
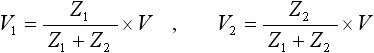
・・・ (16)
これを分圧則と呼んでいます。
一方、図5 (b) は回路素子が並列に接続されており、電流 I が流れている様子を表しています。ここで各素子のアドミタンスを Y1 、 Y2 とすると、それぞれの回路素子に流れる電流は下式(17) の式で与えられます。

・・・ (17)
これを分流則と呼んでいます。これら分圧則と分流則は、覚えておくと非常に便利です。
それでは次節「2-6. 電気回路のまとめ」で、第2章 「電気回路 入門」のまとめと少し補足説明をしたいと思います。