電子回路設計の基礎(実践編)> 5-1. 三角波を作る
三角波を作る
この章では、きれいな三角波を作る方法について学びます。前章で学んだ PWM(Pulse Width Modulation)信号は三角波から作ることができますが、高性能化のためにはきれいな三角波が必要です。
1. 三角波発生回路の作成に必要な部品
「第5章 三角波 発生回路」で使用する部品を表1 にリストアップします。本章で学習するために必要な電子部品です。
| 部品名 | 値 | 数量 |
| 抵抗 | 2.2 kΩ | 3 |
| 抵抗 | 1.5 kΩ | 2 |
| 抵抗 | 33 kΩ | 2 |
| 抵抗 | 200 kΩ | 1 |
| コンデンサ | 0.1 μF | 2 |
| オペアンプ | 2 |
※ 部品の入手方法は実践編 第1章「1-4. 電子部品などの揃え方」をご参照ください。
※ 電圧測定や波形観測のための測定器については同じく第1章「1-3. 必要な工具・測定器」をご参照ください。
前章「4-2. PWM信号を作る」で説明したように、三角波とコンパレータ(比較器)を使って PWM信号を発生させることができます。図1 のようにコンパレータの判定電圧 Vcomp を変化させることにより、様々なデューティー(Duty)の PWM信号を作ることができます。
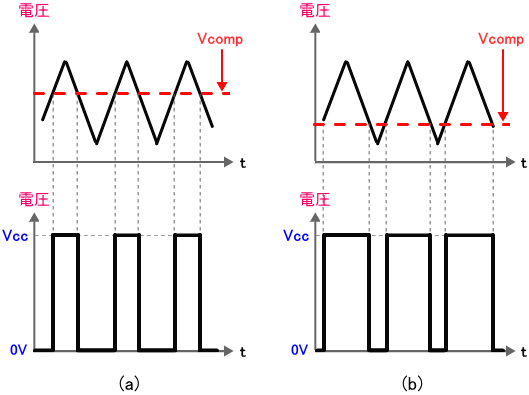
図1. PWM信号の作り方
ここで、Vcomp 電圧の変化に対して線形にデューティーを変化させたい場合、三角波は歪み(ひずみ)がなくきれいである必要があります。PWM信号を発生する回路を構成するとき、高性能化のためにきれいな三角波が必要とされる場合があります。
そこで、この章ではきれいな三角波を作る方法について説明したいと思います。
◆ 本の紹介 (検索もできます。)
○ amazonでネット注文できます。
2. 三角波発生の原理
三角波は、矩形波(方形波)と積分回路を使うことで作ることができます。矩形波については、すでに実践編 第3章「矩形波 発生回路」で説明しました。
ここでは、矩形波を積分して三角波となる原理について説明します。
(積分回路の詳細については「5-2. 積分回路」で紹介します。)
積分は式 (1) のような式で表されます。
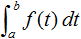
・・・ (1)
式 (1) を図で表したものが図2 です。
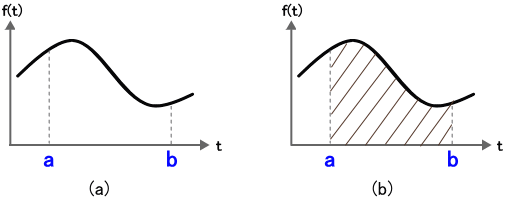
図2. 積分
時間 t の関数 f(t) が図2 (a) のような波形だとすると、式 (1) のように t = a から t = b までの間の積分結果は、図2 (b) の斜線で囲った面積になります。
それでは次に、図3 のようなパルス波形の積分を考えてみましょう。
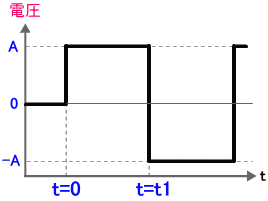
図3. パルス波形
パルス波形は、図3 のように t = 0 以前は f(t) = 0 、t = 0 から t = t1 までの間が f(t) = A だとします。t = 0 以前は f(t) は常に 0 なので、積分の結果も常に 0 です。
図4 (a) のように、時間が t = 0 を少し過ぎた t = tx のときの積分結果は、斜線部の面積である A × tx となります。
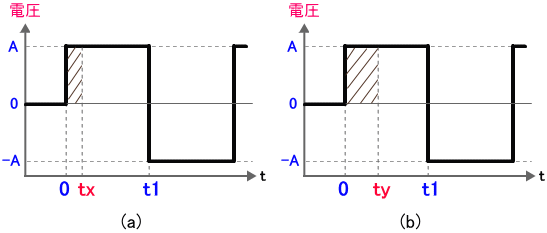
図4. パルス波形を積分する様子 (1)
さらに時間が進んで、t = ty となった時の積分結果は、図4 (b) 斜線部の面積である A × ty となります。結果的に、時間 t = 0 以前から t = t1 までの積分結果 I(t) の動きは図5 のようになります。
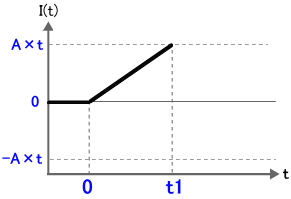
図5. パルス波形を積分する様子 (2)
結果、t = 0 から t = t1 までは I(t) = A/t1 × t となり、時間 t に比例して直線となります。
さらに時間が進んで、t = t1 以降はどのようになるかと言うと、電圧が -A となるため図6 に示すように時間 t に比例して負の傾きで直線に変化していきます。
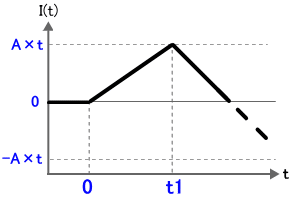
図6. パルス波形を積分する様子 (3)
結果的に、この動作を繰り返すと三角波になります。矩形波(方形波)の繰り返し波形を積分すると、三角波になることを理解して頂けたと思います。
本章では、実践編「第3章 矩形波 発生回路」で作成した矩形波(方形波)発生回路と積分回路(積分器)を使って三角波を発生する回路を作成します。
3. 本章「三角波発生回路」の流れ
このページでは、本章で学習する三角波発生の原理について述べてきました。次のページ以降から具体的に積分回路、三角波発生回路の学習を進めていきます。以下に 5-2. 以降の学習の流れを示します。
- 5-2. 積分回路
- 5-3. 三角波発生回路を作る
「5-2. 積分回路」では、積分回路(積分器)の回路構成や理論式について説明します。
「5-3. 三角波発生回路を作る」では、矩形波(方形波)発生回路と積分回路を使った三角波発生回路の実験を行います。
それでは、以上で述べた内容に従って三角波発生回路を学習していきましょう。