1. 電気回路（回路理論）とは

電気回路で扱う内容は、大きく分けると「直流回路（DC）」と「交流回路（AC）」になります。直流回路および交流回路といった電気回路の解析方法をまとめたものが回路理論です。

直流回路はそれほど難しくはなく、オームの法則を知っていれば基本的には問題ありません。ただし、回路理論を統一的に理解したいのであれば（つまり、交流回路のインピーダンスやアドミタンスを理解したいのであれば）、抵抗に加えてコンダクタンスの考え方を知る必要があります。そうすることにより、電気回路を基礎からしっかりと理解することができるようになります。

交流回路は直流回路とは異なり、電気回路を勉強される方のほとんどが理解に苦しみます。その理由は複素数と呼ばれる数を使うためです。

交流回路の解析とは、正弦波交流（サイン波）に対する解析です。しかし交流回路の計算では、 sin , cos ではなく複素数を使います。実際に、この複素数に対して苦手意識を持っている方もいるでしょう。

複素数とは、実数と虚数を含んだ数のことです。実数は -2.3 , -1 , 0 , 1.7 , 2 といった私たちに馴染みのある数です。一方、虚数とは2乗してマイナスとなる数のことで、実際には存在しない数のことです。

電気回路では2乗して -1 となる数を” j ”と表現します。虚数を含む複素数は、まったくもって得体の知れない数で理解できなくても当然です。そもそも虚数自体には何の意味もなく、交流回路の計算を非常に簡単に行うことができるため用いられているだけなのです。（交流回路と複素数の関係については、「2-3. 交流回路と複素数」で分かりやすく説明します。）

それではまず、本格的に電気回路の説明をに入る前に、直流回路と交流回路の”基礎の基礎”について説明します。

2. 直流回路と交流回路の基礎の基礎

まずは直流回路の基礎について説明します。皆さんはオームの法則はご存知だと思います。中学校、高校の理科で学びましたよね。オームの法則は、抵抗という素子の両端にかかる電圧を V 、そのとき抵抗に流れる電流を I とすると式(1) のように求まります。

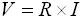
・・・ (1)

このとき、 R は抵抗の値を表します。「抵抗」とは、その名の通り電流の流れに対して抵抗となる素子です。つまり、抵抗の値 R は電流の流れを妨げる度合いを表しています。直流回路に関しては式(1) を理解できれば十分なのですが、先ほど述べたように回路理論を統一的に理解したいのであれば抵抗に加えてコンダクタンスの考え方を理解する必要があります。コンダクタンスは抵抗の逆数で G=1／R と表されます。そうすると式(1) は下式(2) のように表すことができます。

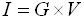
・・・ (2)

抵抗値が「電流の流れを妨げる度合い」であれば、コンダクタンスの値は「電流が流れやすい度合い」ということになります。

詳細はこのページの「4. 回路理論における直流回路の計算」で述べますが、抵抗とその逆数であるコンダクタンスを用いた式(1) と式(2) を用いることにより、電気回路の計算をパズルのように解くことができます。このことは交流回路の計算方法にもつながることですので、電気回路の”基礎の基礎”として覚えておいてください。

次に、交流回路の基礎について説明します。交流回路では角速度（または角周波数ともいう） ω 、振幅 A の正弦波交流（サイン波）の入力 A×sin(ωt) に対して、出力がどのようになるのかを解析します。 t は時間を表します。交流回路で扱う素子は抵抗に加えて、容量（コンデンサ）やインダクタ（コイル）といった素子が登場します。それぞれの回路記号は以下の図1 のように表されます。

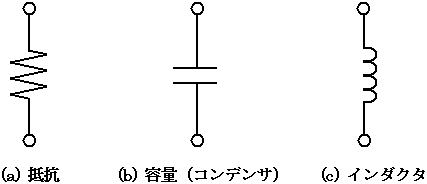
図1. 回路記号

これらの素子で構成された回路は、正弦波交流の入力 A×sin(ωt) に対して振幅と位相のみが変化するというのが特徴です。つまり交流回路は、図2 の上図のような入力に対して、出力の振幅の変化と位相のずれのみが分かれば入力と出力の関係が分かるということになります（図2 の下図）。

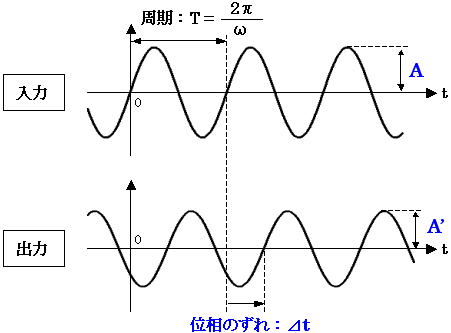
図2. 入力に対する位相と振幅の変化

ちなみに角速度（角周波数） ω （単位：rad/s）と周波数 f （単位：Hz）の関係ですが、下式(3) のように表されます。

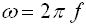
・・・ (3)

また、周期 T （単位：s）は周波数 f の逆数であるため、下式(4) のように表されます。

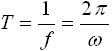
・・・ (4)

先ほども述べた通り、交流回路では入力に対する出力の振幅と位相の変化量が分かればよく、交流回路の計算では複素数を用いて振幅と位相の変化量を求めます。この複素数を用いることによって交流回路の計算は非常に簡単なものになるのです。

以上が交流回路の基礎になります。交流回路については、次節以降で再び説明することにします。

それでは次に、抵抗とコンダクタンスを使った直流回路の計算について説明します。抵抗とコンダクタンスを使った計算は交流回路の計算の基礎にもなるものですが、既にご存知の方は次節、「2-2. 容量とインダクタ」に進んで頂いても構いません。

3. 直流回路の計算

本節の「1. 電気回路（回路理論）とは」で述べたように、回路理論では直流回路の計算において抵抗に加えてコンダクタンスという考え方が出てきます。ここではコンダクタンスの話をする前に、まずは中学校、高校の理科で学んだことを復習してみましょう。

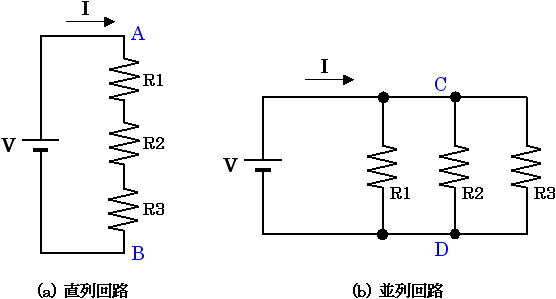
図3. 抵抗で構成された直列回路と並列回路

中学校、高校の理科では、抵抗と電流、電圧の関係であるオームの法則を学んだと思います。オームの法則は V = R × I で表されます。図3 の回路を解いてみます。同図(a) は抵抗が直列に接続されていています。まずは合成抵抗を求めます。A点-B点間の合成抵抗 Rtotal は下式(5) のようになります。

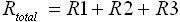
・・・ (5)

直列に接続された抵抗の合成抵抗は、単純に抵抗値を足すだけで求めることができます。よって図3 (a) の回路に電圧 V を与えたときに流れる電流は下式(6) のように求められます。

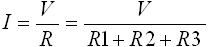
・・・ (6)

一方、図3 (b) は抵抗が並列に接続されています。C点-D点間の合成抵抗 Rtotal は下式(7) のように求めることができます。

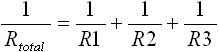
・・・ (7)

並列に接続された抵抗の合成抵抗についてですが、各抵抗の逆数 1/R1 、 1/R2 、 1/R3 の和は合成抵抗の逆数 1/Rtotal となります。よって、合成抵抗 Rtotal は下式(8) となります。

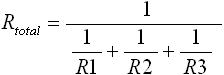
・・・ (8)

図3 (b) の回路に電圧 V を与えたときに流れる電流は下式(9) のように求められます。

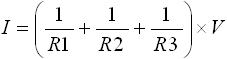
・・・ (9)

以上が中学校、高校の理科で学んだことの復習です。それでは次に回路理論における直流回路の計算方法について説明します。

4. 回路理論における直流回路の計算

回路理論では、いくつかの「決まり事」を用いてパズルのような感じで電気回路の計算を行うことができます。このことは交流回路の計算にも通じることです。まずはパズルのように解く方法を、直流回路の計算で習得しましょう。

まずは、コンダクタンスという考え方を理解しましょう。コンダクタンスは抵抗 R の逆数で、コンダクタンスを G とすると G=1/R となります。式(7) をコンダクタンスを用いて表すと以下のようになる。

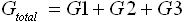
・・・ (10)

式(10) を見ると分かるように、並列に接続された抵抗の合成コンダクタンスは各コンダクタンスの単純な足し算で求めることができます。

さて、それでは回路の計算をパズルのように行うための「決まり事」について説明します。「決まり事」は以下の通りです。

決まり事(1) ・・・ 求めるものが電圧か電流かで合成抵抗 Rtotal か合成コンダクタンス Gtotal のどちらを求めるか決める。
・ 求める値が電圧の場合 ： V = Rtotal × I の合成抵抗 Rtotal を求める。
・ 求める値が電流の場合 ： I = Gtotal × V の合成コンダクタンス Gtotal を求める。

決まり事(2) ・・・ 直列接続なら合成抵抗、並列接続なら合成コンダクタンスを求める。
・ 抵抗が直列接続されている場合 ： 合成抵抗 Rtotal = R1+R2+R3+・・・ を求める。
・ 抵抗が並列接続されている場合 ： 合成コンダクタンス Gtotal = G1+G2+G3+・・・ を求める。

決まり事(3) ・・・ 抵抗 R とコンダクタンス G の変換は、お互いを逆数にする。（ R = 1／G , G = 1／R ）

それでは、以上の決まり事を使って図3 の回路をもう一度解いてみましょう。同じ回路を図4 に示します。

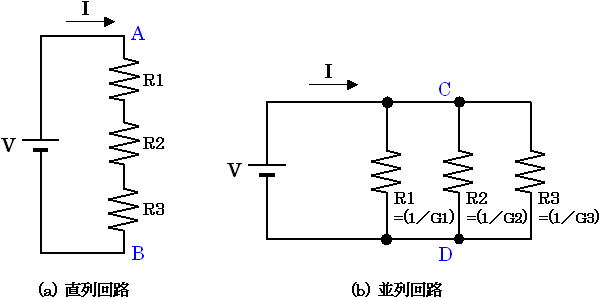
図4. 図3の回路

まず図4 (a) について解いてみます。電圧 V が与えられており、求めるものは電流 I であるため「 決まり事(1) 」より I = Gtotal × V の Gtotal を求めます。つまり、A点-B点間の合成コンダクタンス Gtotal を求めます。

次に、A点-B点間の抵抗 R1, R2, R3 に注目します。抵抗は直列に接続されているため、「 決まり事(2) 」より合成抵抗 Rtotal を求めます。 Rtotal = R1 + R2 + R3 となります。

さて、始めに「 決まり事(1) 」より、求めるものが電流 I であることから合成コンダクタンスを求めると述べました。そこで「 決まり事(3) 」を使って合成抵抗 Rtotal = R1 + R2 + R3 を合成コンダクタンスに変換します。合成コンダクタンスは下式(11) となります。

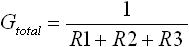
・・・ (11)

よって、 I = Gtotal × V に式(11) を代入することにより、式(6) と同じ式を得ることができます。

次に図4 (b) について解いてみます。こちらも「 決まり事(1) 」より I = Gtotal × V の Gtotal を求めます。そしてC点-D点間の抵抗 R1, R2, R3 に注目すると、並列に接続されているため「 決まり事(2) 」より合成コンダクタンス Gtotal は Gtotal = G1 + G2 + G3 となります。よって、 I = Gtotal × V より下式(12) が求まります。

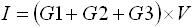
・・・ (12)

式(12) に G1=1/R1, G2=1/R2, G3=1/R3 を代入すると、式(9) と同じ式を得ることができます。

回路理論の計算は理解できたでしょうか？それでは最後にもう一つ、図5 (a) の回路を解いてみましょう。

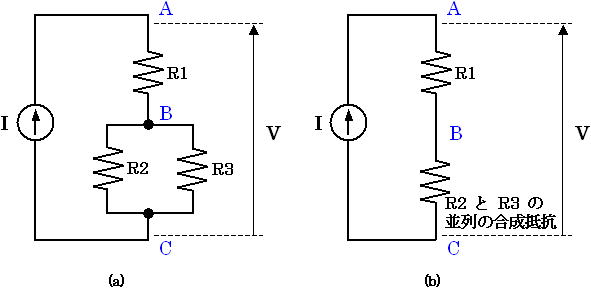
図5. 直流回路の例題

この図5 (a) の回路は電流 I が与えられており、求めるものは電圧 V であるため「 決まり事(1) 」より V = Rtotal × I の Rtotal を求めます。つまり、A点-C点間の合成抵抗 Rtotal を求めることになります。

まず、B点-C点間の抵抗 R2 、 R3 に注目します。並列に接続されているため、「 決まり事(2) 」より合成コンダクタンスを求めます。B点-C点間の合成コンダクタンス G2,3 は下式(13) のようになります。

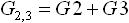
・・・ (13)

そうすると、合成コンダクタンス G2,3 は図5 (b) のように1つの抵抗と考えることができます。ここで、「 決まり事(3) 」を使って合成コンダクタンス G2,3 を抵抗 R2,3 に変換します（式(14) ）。

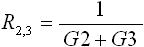
・・・ (14)

次に、A点-C点間の抵抗 R1 と 式(14) の R2,3 に注目すると、直列に接続されていることが分かります。よって、「 決まり事(2) 」より合成抵抗 Rtotal を求めればよく、 Rtotal = R1 + R2,3 となります。

始めに、「 決まり事(1) 」より求めるものが電圧 V であることが分かっていますから、 V = Rtotal × I を求めます。そうすると下式(15) を得ることができます。

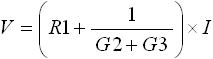
・・・ (15)

最後に、式(15) に G2=1/R2 、 G3=1/R3 を代入し下式(16) を得ます。

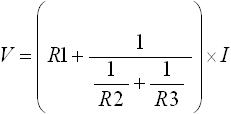
・・・ (16)

以上が、抵抗とコンダクタンスを用いた直流回路の計算です。パズルのような感じで電気回路の計算を行う方法が分かったと思います。

それではいよいよ次節、「2-2. 容量とインダクタ」から交流回路（交流理論）についての説明を行っていきます。