1. 矩形波（方形波）発生回路の周波数の式

図1 がこれまでに作成した矩形波（方形波）発生回路の回路図です。前ページ「3-5. RC回路と時定数」では、抵抗 R4 の値とコンデンサ C1 の値によって下図の回路の周波数が決まることが分かりました。

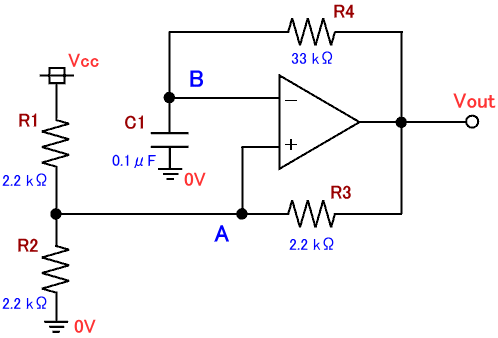
図1. 矩形波（方形波）発生回路

このページは実験のページではありません。数式を計算して周波数の理論式を求めるため、少し難しい部分もあるかもしれませんが、興味がある方はご覧ください。

それでは、図1 の矩形波（方形波）発生回路について、周波数の理論式を求めて行くことにしましょう。まず、Vout の電圧が 0V → Vcc に変化したときの B点の電圧について考えていきましょう。

前ページ「3-5. RC回路と時定数」で述べた通り、RC回路の出力である B点の電圧は式 (1) に従います。

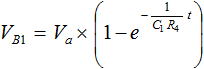
・・・ (1)

ここで、Va は 1／3 × Vcc から Vcc までの電圧です。

Vout の電圧が 0V → Vcc に変化するタイミングは、B点の電圧が 1／3 × Vcc のときです。そのため B点の電圧は 1／3 × Vcc から Vcc に向けて図2 のように変化します。

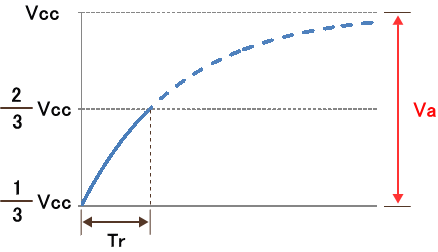
図2. B点の電圧の立ち上がり

何もなければ、このまま図2 に示す点線に沿って Vcc まで電圧が上昇するのですが、B点の電圧が 2／3 × Vcc になったとき Vout の電圧は Vcc → 0V に変化します。

ここで、図2 の Tr の時間を求めることにします。時間 Tr のときの電圧は 1／2 × Va ですので、式 (1) から式 (2) を求めることができます。

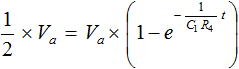
・・・ (2)

式 (2) を変形していくと式 (3) 、式 (4) となります。

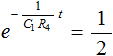
・・・ (3)

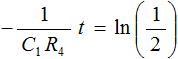
・・・ (4)

よって、時間 t は下式のように求まります。

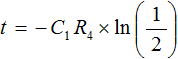
・・・ (5)

ln(1/2) = -0.693 ですので、時間 t は最終的に式 (6) のようになります。

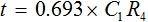
・・・ (6)

つまり、式 (6) が図2 の Tr になります。Tr の式を改めて式 (7) に示します。

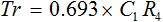
・・・ (7)

それでは次に、Vout の電圧が Vcc → 0V に変化したときの B点の電圧について考えていきましょう。RC回路の出力である B点の電圧は式 (8) に従います。

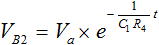
・・・ (8)

ここで、Va は 2／3 × Vcc から 0V までの電圧です。

Vout の電圧が Vcc → 0V に変化するタイミングは、B点の電圧が 2／3 × Vcc のときです。そのため B点の電圧は 2／3 × Vcc から 0V に向けて図3 のように変化します。

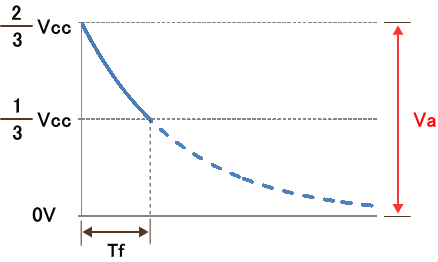
図3. B点の電圧の立ち下がり

何もなければ、このまま図3 に示す点線に沿って 0V まで電圧が上昇するのですが、B点の電圧が 1／3 × Vcc になったとき Vout の電圧は 0V → Vcc に変化します。

ここで、図3 の Tf の時間を求めることにします。時間 Tf のときの電圧は 1／2 × Va ですので、式 (8) から式 (9) を求めることができます。

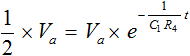
・・・ (9)

式 (9) を先ほどと同じように解くと、時間 t は式 (6) と同じになります。つまり、図3 の Tf は式 (10) になります。

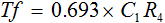
・・・ (10)

以上より、図4 のように矩形波（方形波）発生回路の 1周期の時間が分かります。

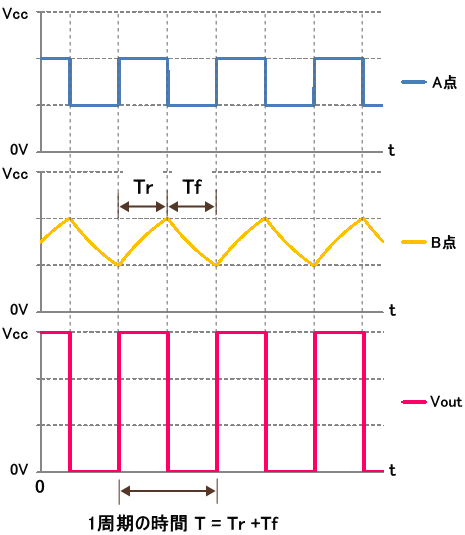
図4. 矩形波（方形波）発生回路の 1周期の時間

1周期の時間 T は下式のようになります。

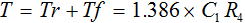
・・・ (11)

周波数 f は周期の逆数で求めることができるので、周波数 f = 1/T となります。よって、矩形波（方形波）発生回路の周波数の式は下式になります。

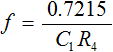
・・・ (12)

それでは次に、式 (12) の理論式と実際の回路の周波数を確認してみましょう。

2. 周波数の式と実際の動作の比較

先ほど「1. 矩形波（方形波）発生回路の周波数の式」で求めた数式と、実際の回路の動作を比較してみましょう。

式 (13) が先ほど求めた矩形波（方形波）発生回路の周波数 f の式です。

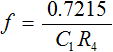
・・・ (13)

この式に R4 = 33 kΩ、C1 = 0.1 μF を代入すると下式のように 218.6 Hz となります。

図5 は「3-4. 矩形波（方形波）発生回路」で作成した矩形波（方形波）発生回路の出力波形です。

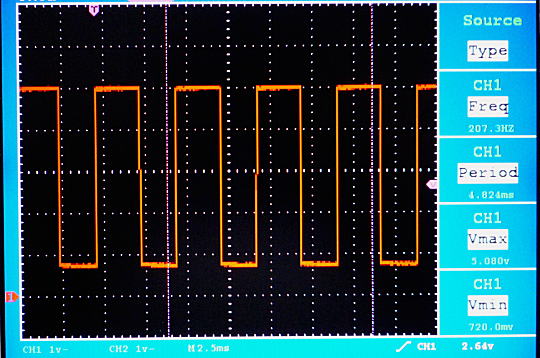
図5. オシロスコープの画像

周波数は上図のように 207.3 Hz となっており、ほぼ理論式から求めた値と等しいことが分かります。式 (13) を使えば、目標の周波数にするためは抵抗 R4 とコンデンサ C1 の値をどの様に設定すればいいかが分かります。