電子回路設計の基礎 > 2-3. 交流回路と複素数
交流回路と複素数
交流回路の解析である交流理論では複素数を使います。複素数を使う理由を一言で言うとしたら、交流回路の計算を簡単に行うことができるからです。交流回路に正弦波交流(サイン波)を入力すると、出力の振幅と位相のみが変わる、と以前にも述べました。この振幅と位相の変化の様子は、複素数の足し算や掛け算で簡単に表現することができるのです。
このページでは、まず交流回路と密接な関係にある複素数の特徴について説明していきます。
1. 正弦波と等速円運動
交流回路の計算(交流理論)と複素数は、非常に密接な関係にあります。その関係について話をしようと思うのですが、その前に、まず正弦波(サイン波)と等速円運動の関係について述べます。
交流回路は入力される正弦波に対して、振幅と位相のみが変化するという特徴を持ちます。正弦波というのは、時間の経過とともに図1 のような波形となるものをいいます(横軸 t が時間)。交流回路では、入力に対する出力の振幅の変化と位相のずれについて解析を行います。
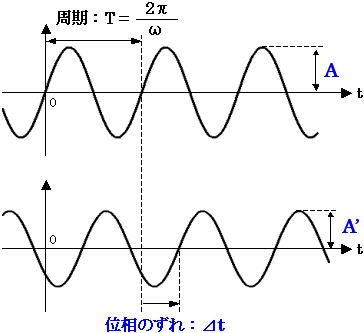
図1. 正弦波(サイン波)
図1 の上図は、「2-1. 電気回路の基礎」で述べたように下式(1) で表されます。
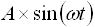
・・・ (1)
この式(1) を入力と考え、出力が図1 の下図のように振幅が変化して位相がずれたと考えると下式(2) のようになります。
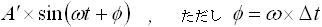
・・・ (2)
さて、正弦波と等速円運動の関係について述べたいと思います。図2 (a) は角速度(または角周波数) ω で等速円運動している様子を表しており、この等速円運動の縦軸の値 y を時間の経過とともに描いたものが同図 (b) です。
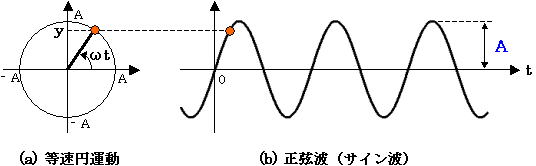
図2. 等速円運動と正弦波の関係
このように、正弦波は等速円運動しているものを縦軸に投影したときの動作と等しいのです。ここで入力である式(1) の正弦波を基準として考えるため、時間 t=0 のときの式(1) と式(2) を図2 (a) のように表すと図3 のようになります。
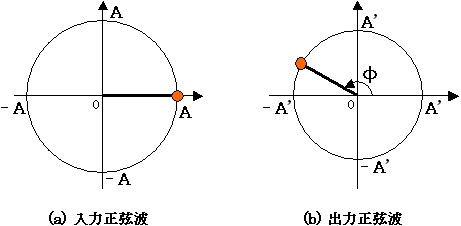
図3. 入力と出力の位相と振幅の関係
図3 を見ると、振幅 A の入力正弦波に対して、出力正弦波は振幅が A' となり位相が入力に対して Φ 進んでいることが一目瞭然で分かります。交流回路では、入力に対して出力の振幅と位相のみが変化すると述べましたが、その様子を図3 のようにして表すことが可能なのです。
交流理論では複素数を用いて計算すると述べましたが、具体的には図3 の横軸を実数軸、縦軸を虚数軸とすることにより交流回路を表すことができます。それでは、次に複素数の特徴について説明したいと思います。
◆ 初心者におすすめの本 - 図解でわかるはじめての電気回路
- 説明の図も多く、分かりやすいです。
- これから電気回路を学ぶ方にお勧め、初心者必見の本です。説明がかなり丁寧です。
- 容量の原理について、クーロンの法則や静電誘導の原理といった説明からしっかりとされています。
- インダクタの原理について、ファラデーの法則やフレミングの法則といった説明からしっかりとされています。
- インピーダンスとアドミタンスについても、各素子に関して丁寧に説明されています。
- 抵抗、容量、インダクタ、トランスの説明
- インピーダンスやアドミタンスの説明、計算方法
- 三相交流の説明
- トランジスタやダイオードといった半導体素子の説明と正弦波交流に対する動作
○ amazonでネット注文できます。
◆ その他の本 (検索もできます。)
2. 複素数とは
複素数とは、実数と虚数を含んだ数のことで、a + jb (a:実数、jb:虚数)というように表されます。 j は2乗すると -1 となる数です。つまり下式(3) となります。
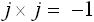
・・・ (3)
このような特徴を実際に持つ数など存在しません。そのため虚数と呼ばれているのですが、非常に重要な特徴なのです。実数を横軸、虚数を縦軸として表現すると、 a + jb は図4 のようになります(以降、横軸を実軸、縦軸を虚軸と呼ぶことにします)。
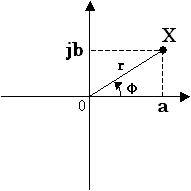
図4. 複素数の表現
このとき、原点から実軸 a と虚軸 jb で表される点 X までの距離 r は下式(4) のようになります。
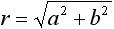
・・・ (4)
また、実軸と原点-X点を結ぶ直線とでなす角 Φ は以下のように求まります(式(5) )。
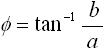
・・・ (5)
先ほどの「1. 正弦波と等速円運動」で述べたことに当てはめると、正弦波の振幅が式(4) で位相のずれが式(5) に当たります。
3. 複素数の計算
さて、それでは次に複素数の足し算、引き算や掛け算、割り算の特徴についてみていきましょう。複素数の計算の特徴は、交流回路の振幅と位相の変化を表すことができるため、非常に重要な特徴となります。
まず複素数 a + jb と c + jd の足し算、引き算について考えてみます。式を解くと足し算は式(6) 、引き算は式(7) のようになります。
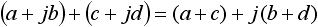
・・・ (6)
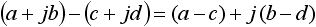
・・・ (7)
これを実軸と虚軸の図で表すと、図5 のようになります。図5 (a) の Z点が足し算の結果、図5 (b) の Z点が引き算の結果となります。
(引き算は、 ( a + jb ) - ( c + jd ) = ( a + jb ) + ( -c - jd ) と表すことができます。)
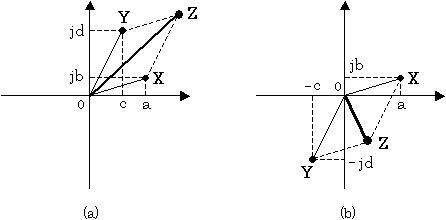
図5. 複素数の計算(足し算、引き算)
図5 より分かる通り、複素数の足し算、引き算はベクトル計算のような特徴を持ちます。
次に掛け算、割り算の特徴について述べます。 a + jb の原点からの距離、および実軸とのなす角をそれぞれ下式(8) のように r1 、 Φ1 とします。
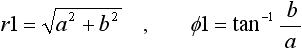
・・・ (8)
また、 c + jd についても同様に、原点からの距離、および実軸とのなす角をそれぞれ下式(9) のように r2 、 Φ2 とします。
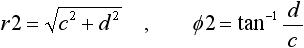
・・・ (9)
以下、計算は省略することにしますが、複素数の掛け算 ( a + jb ) × ( c + jd ) の結果は図6 (a) のように原点からの距離は r1×r2、実軸とのなす角は Φ1 + Φ2 となります。
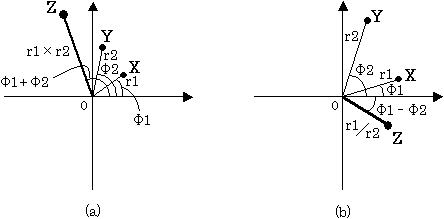
図6. 複素数の計算(掛け算、割り算)
また、割り算 ( a + jb )/( c + jd ) の結果は図6 (b) のように原点からの距離は r1/r2、実軸とのなす角は Φ1 - Φ2 となります。
以上が複素数の計算の特徴です。複素数の足し算、引き算や掛け算、割り算は、交流回路の特徴を表すのに適しています。それでは次節「2-4. インピーダンスとアドミタンス」で、交流回路の計算で重要なインピーダンスとアドミタンスの考え方について説明します。インピーダンスとアドミタンスは複素数で表されます。