1. フィードバックとは

フィードバックとは、出力の目標値と実際の出力値を比較して自動的に出力値と目標値が一致するように制御する仕組みのことを言います。フィードバックの意味を分かりやすく言うなら、出力を目標の値に一致させるための制御方法と言えると思います。

これまで制御工学の考え方や伝達関数といった内容について説明してきましたが、制御工学では、フィードバック制御されたシステムの伝達関数を求めることにより安定したシステムを設計することができるようになります。

図1. アップダウンの道を走行する自動車

このページでは図1 のような図を使って、フィードバック制御の仕組みと安定性の問題についてイメージ的に分かるように説明していきたいと思います。この図1 はアップダウンのある道を車が走行している様子を表しています。この車には速度メーターが付いており、実際の走行速度を知ることができます。

さてここで、この車が時速 60 km の一定速度で走行できるように、自動的に制御することを考えてみましょう。フィードバック制御の目標値は時速 60 km と考えることができ、また、出力が速度メーターの値と考えることができます。

自動的に一定速度で走行するための制御方法ですが、出力の速度メーターの値を読み取りアクセルを調節するようにします。速度が落ちてくるとアクセルを踏み、速度が上がればアクセルを緩めるように制御します。つまり、上り坂のときには車の速度が落ちるのでアクセルを踏むようにします。逆に下り坂のときはアクセルを緩めるようにします。

このように制御することにより、図2 に示すようにアクセルを踏んだり緩めたりしながら、自動的に時速 60 km の一定速度で走行することが可能となります。

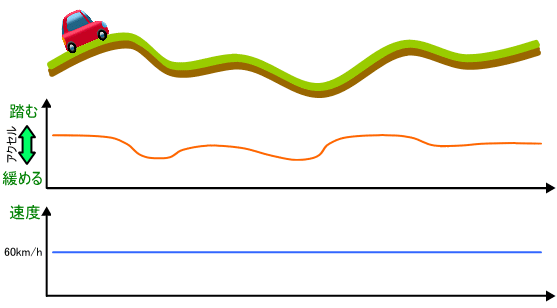
図2. 一定の速度で走行する自動車

以上で説明したようにフィードバックとは、出力の目標値と実際の出力値を比較して自動的に出力値と目標値が一致するように制御する仕組みのことをいいます。

しかし、今までの説明は理想的な状態です。実際には、速度メーターを読み取り車のアクセルを調整するまでの間に時間差が発生します。このことが場合によって不安定な状態を導くことがあります。

それでは次に、なぜフィードバック制御が不安定になってしまうのかについて説明します。

2. フィードバック制御が不安定になる原因

フィードバック制御を行うことにより、出力を目標の値に安定させることができることは先ほど述べました。しかし、このフィードバック制御は気を付けないと不安定になってしまい、場合によっては暴走してしまうことがあるのです。ここでは、不安定になってしまう原理について先ほどの車の例を使って考えてみたいと思います。

「1. フィードバックとは」の説明では考慮しませんでしたが、フィードバック制御では出力の値と目標値と比較して、出力を調整するまでに実際には少し時間差が発生してしまいます。このことを踏まえてもう一度、図2 の例を書き直すと図3 のようになります。

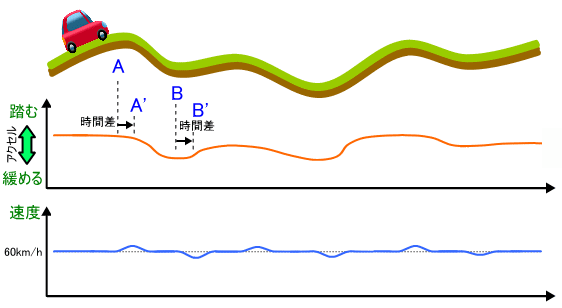
図3. 時間差を含んだフィードバック制御のイメージ

図中 A点から徐々に速度が上がり始めますが、実際にアクセルを調整し始めるまでに時間差があり、A'点まで移動した後にアクセルを緩めて時速 60 km に戻そうとします。また、 B点から徐々に速度は落ち始めますが、時速 60 km に戻そうとし始めるのは B'点からになります。

速度が上がったり下がったりすると、その都度、アクセルを調整し時速 60 km に戻している様子が分かります。実際には常に時速 60 km ではなく、多少、速度にゆらぎが発生します。以上の例は、フィードバック制御が安定している例を表しています。

それでは今度は、時速 120 km で走行した場合について考えます。速度が先ほどの2倍になったので、実際にアクセルで調整するまでに車は 2倍の距離進んでしまいます。

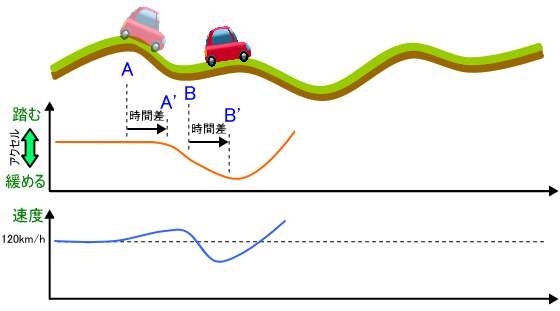
図4. フィードバック制御が不安定になってしまうイメージ (1)

時速 120 km で走ったとき、例えば図4 のように、 A点で速度が上がり始めて A'点で実際にアクセルを緩め始めるのですが、この A'点から上り坂が始まってしまうと速度が急激に落ちてしまいます。さらに B点は上り坂なのでアクセルを踏もうとしますが、実際にアクセルを踏み始めるのは B'点からです。もし、この B'点から下り坂が始まってしまえば、今度は逆に急激に速度が上がってしまいます。

このようなことを繰り返してしまうと図5 に示すように、車の速度は大きく変化を繰り返してしまい最終的には制御不能に陥ってしまいます。

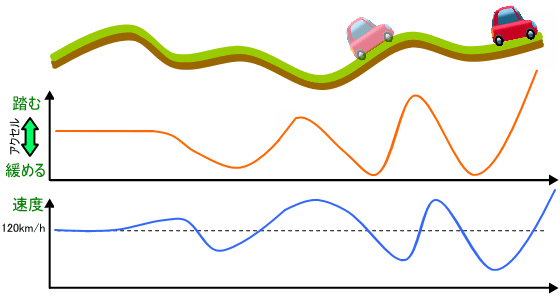
図5. フィードバック制御が不安定になってしまうイメージ (2)

以上で説明してきたように、フィードバック制御は出力を安定させることができますが、場合によっては暴走してしまうことがあります。ここで説明した車の例だけではなく、フィードバック制御を用いたシステムは必ず不安定になってしまう危険性をはらんでいます。

システムが決して不安定にならないようにするには、伝達関数を求めて理論的に常に安定動作するように設計する必要があります。

3. フィードバック制御の伝達関数の求め方

フィードバック制御を行っているシステムの安定性を解析するためには、伝達関数を求める必要があります。本サイトでは安定性の判別法については述べていませんが、フィードバック制御の伝達関数の求め方についてはこれから説明したいと思います。

図6 は最も簡単に表現したフィードバック制御のブロック図です。入出力システムの伝達関数 H(s) があり、その出力を伝達関数 G(s) のフィードバック要素を使って入力に帰還（フィードバック）されています。入力の値は IN 、出力の値は OUT で、伝達関数 OUT/IN を求めます。

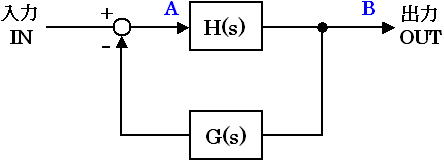
図6. フィードバック制御のブロック図

このようなブロック図の伝達関数を求める場合、図中の A点と B点に注目します。まず A点での値は、入力 IN と G(s) の出力の引き算となります。 G(s) の出力は G(s)×OUT となるので、A点では下式(1) のようになります。

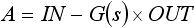
・・・ (1)

次に B点についてですが、 B点は H(s) の出力で下式(2) のようになります。

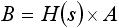
・・・ (2)

B はすなわち OUT です。また、式(2) に式(1) を代入すると下式(3) を得ます。

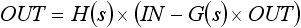
・・・ (3)

さらに式(3) を変形すると式(4) になり、伝達関数 OUT/IN は式(5) のように求まります。

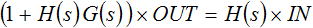
・・・ (4)

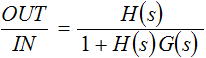
・・・ (5)

以上がフィードバック制御の伝達関数になります。